面積の話です。
素朴な面積の理論(ジョルダン測度)
我々が小学校以来親しんでいる面積の概念を定式化したものが「ジョルダン測度」と呼ばれる面積の測り方です。高校で学ぶリーマン積分も、このジョルダン測度の考えを元に定義されています。
次のような図形\( A \)の面積を図りたい場合、素朴な考えとして正方形のタイルの面積の和として近似する方法が考えられます。

以下は一定の大きさの正方形のタイルで図形の内側から近似してみた例。小学校で円の面積の話をするときとか、あるいは数3の区分求積法と同じようなノリですね。
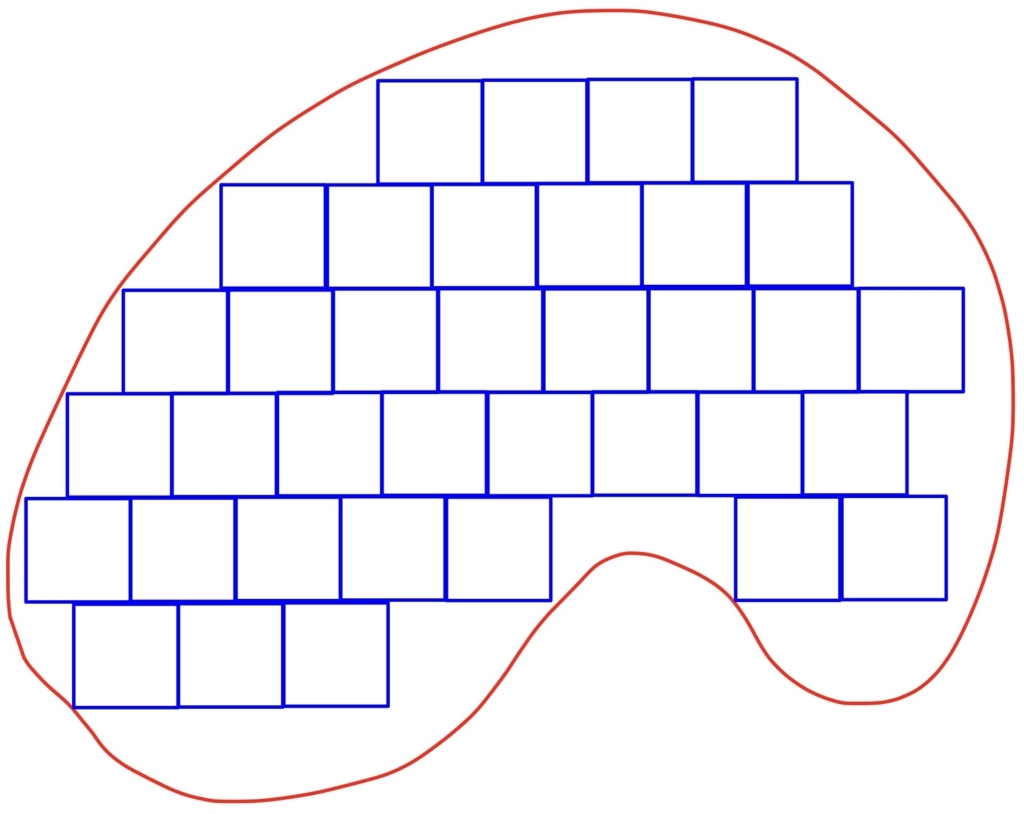
もちろん、そのままだとスキマのせいで我々の考える”面積”よりちょっと小さいですから、正方形のタイルの一辺の幅を小さくすることで近似をよくしていきます。
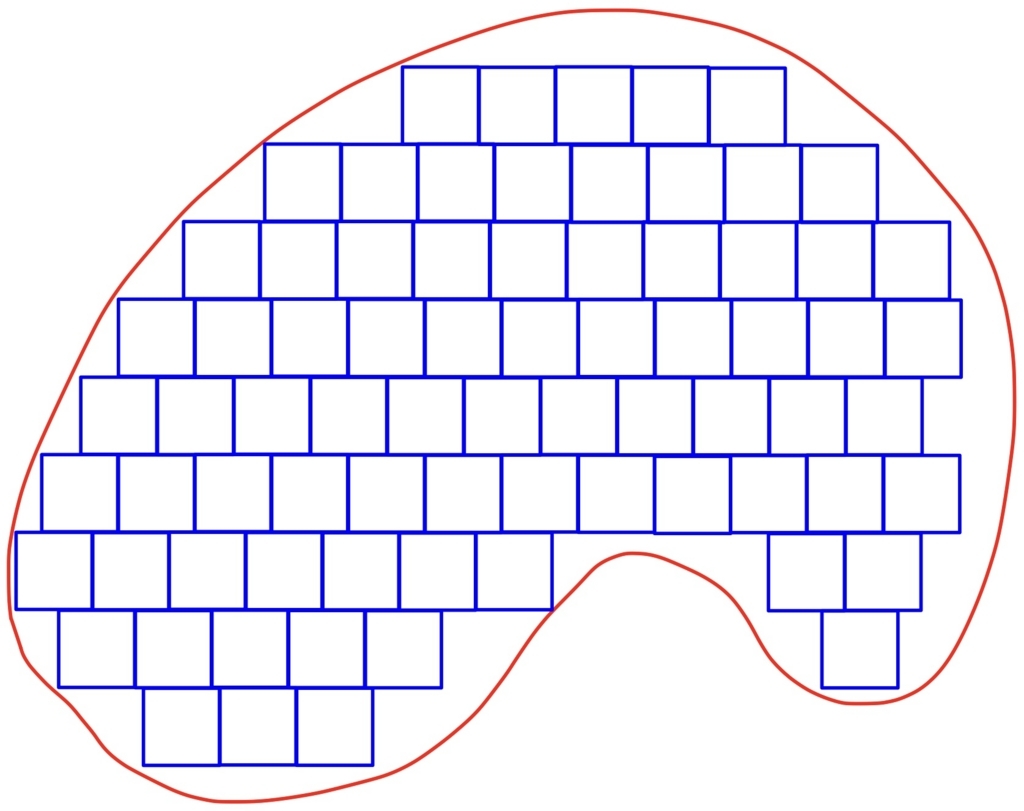
一辺が\( \varepsilon \)の正方形を図形\( A \)内に敷き詰める方法はいろいろありますが、その中で最も多くの枚数をしっける敷き方を考え、そのときの正方形の面積の総和を
\( \displaystyle c_{\varepsilon}(A) \)
とかきます。一般にはこの\( \varepsilon \)を小さくすればするほどスキマが小さくなり、近似が良くなっていきそうです。それらの近似のうち、\( \displaystyle c_{\varepsilon}(A) \)がもっとも大きくなるものを考えます。すなわち
\( \displaystyle c(A)=\sup_{\varepsilon \gt 0}c_{\varepsilon}(A) \)
とおき、これをジョルダン内容量とよぶことにします。
ジョルダン内容量は図形を内側から測定しましたが、図形を覆うような形で外側から面積を測定しようとするのがジョルダン外容量です。
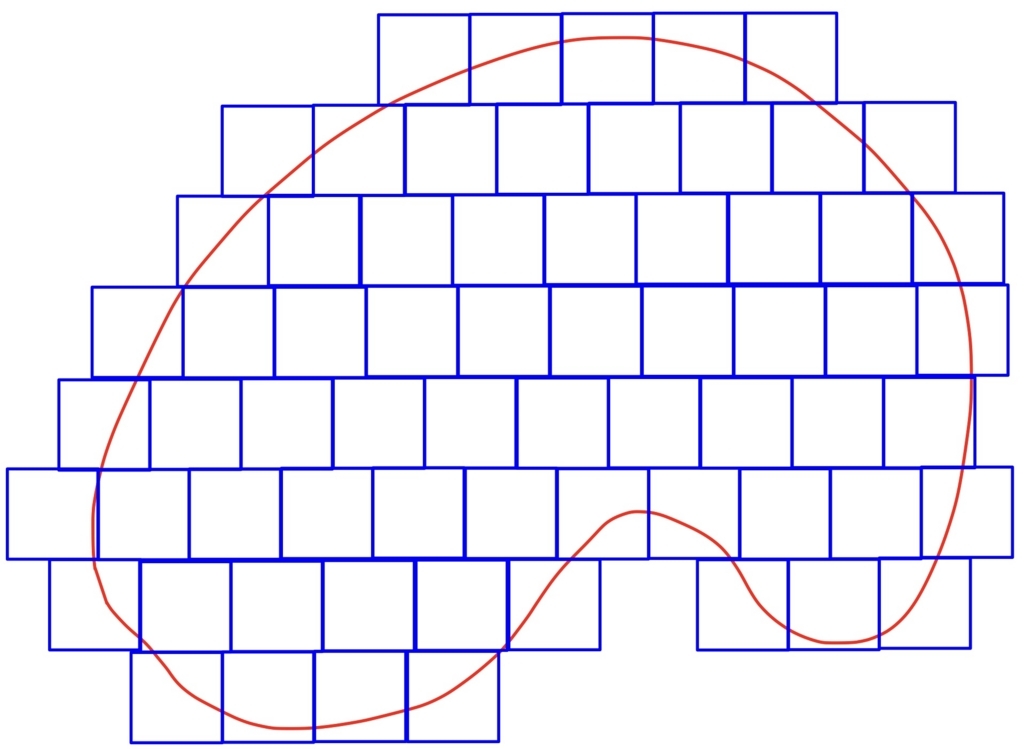
一辺\( \varepsilon \)の正方形を使って\( A \)を(外から)覆う方法のうち、最も使う正方形が少ないものを\( \displaystyle C_{\varepsilon }(A)\)とかき、
\( \displaystyle C(A)=\inf_{\varepsilon \gt 0}C_{\varepsilon }(A) \)
をジョルダン外容量とよびます。
定め方から、
\( \displaystyle c(A)\leq C(A) \)
となります
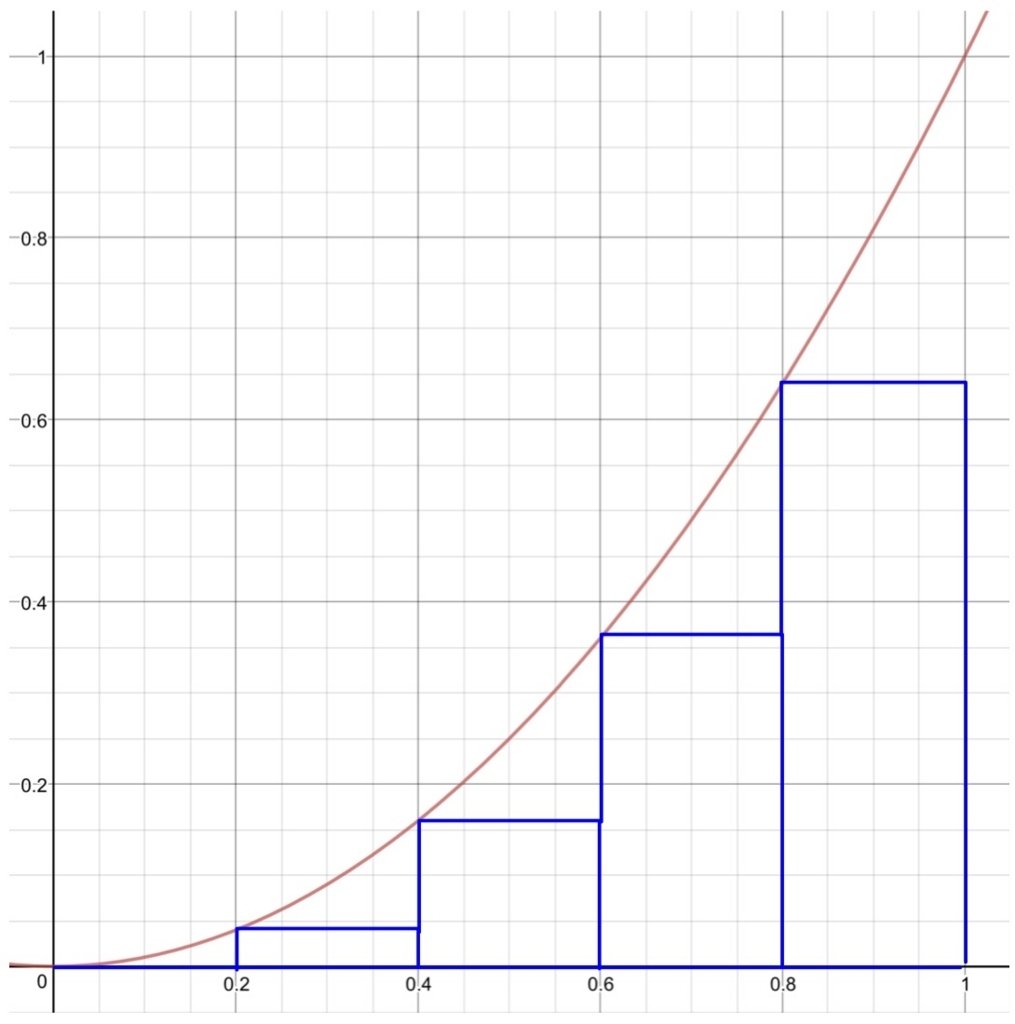
図形の面積を内側から攻めたものと外側から攻めたものがそれぞれジョルダン内容量\( c(A) \)、ジョルダン外容量\( C(A) \)となるわけですが、多くの場合、それらは一致しそうです。よくみる区分求積法の図なんかでも連続関数であれば実際の図形の内側から近似したもの(下左図)と、外側から近似したもの(下右図)は、分割を細かくすれば一致しますよね。
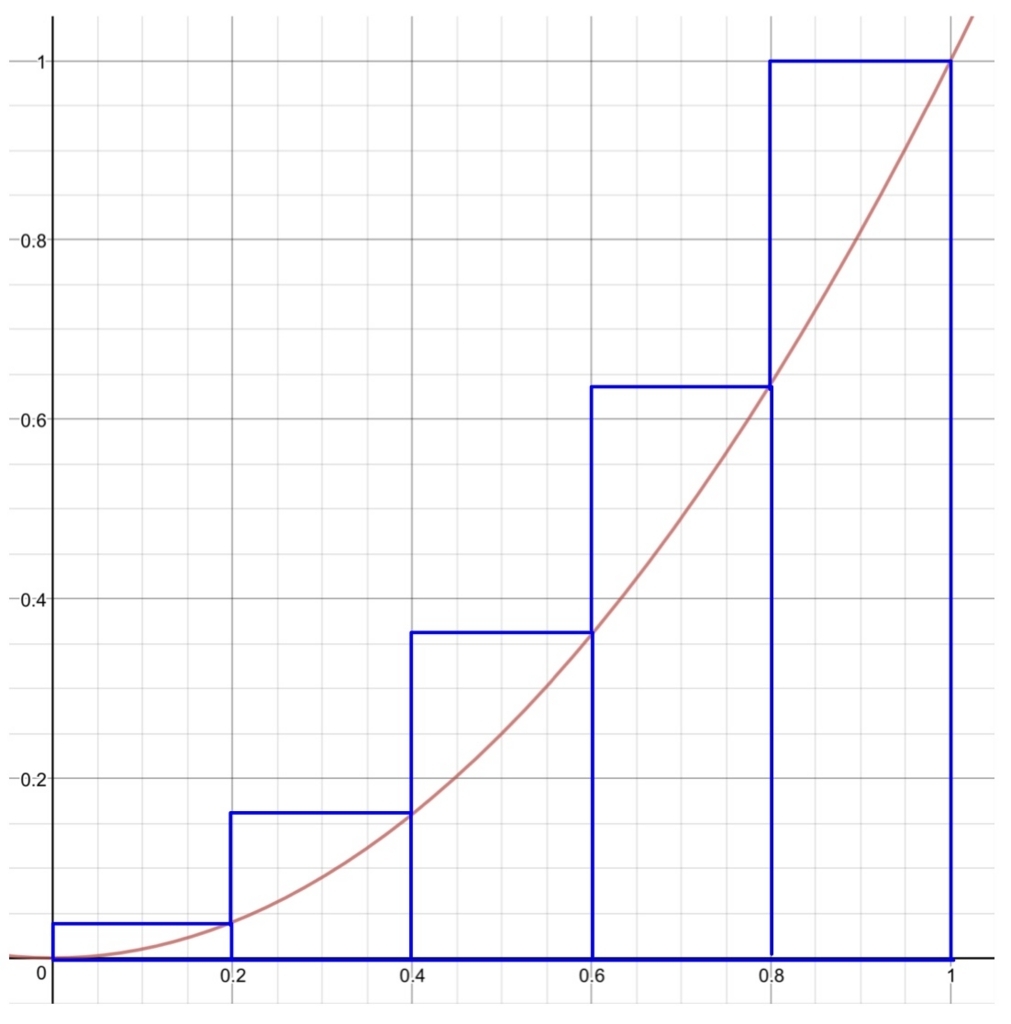
ジョルダン内容量と外容量が一致する、すなわち
\( c(A)=C(A) \)
となるとき、図形\( A \)はジョルダン可測といい、その値\( c(A) \)(あるいは\( C(A)\))を面積というのです。
世の中ジョルダン測度だけではうまくいかない
さて、上のジョルダン測度だと限界が来てしまう例を一つあげましょう。ハルナック集合とよばれる図形です。一辺1の正方形\( H_0 \)から幅が\( \displaystyle \frac14 \)の十字部分を取り除いたものを\( \displaystyle H_1 \)、\( H_1 \)の4つの正方形それぞれから幅\( \frac{1}{4^2}\)の十字部分を取り除いたものを\( H_2 \)とし、以下同様に\( H_3, H_4,\cdots \)を定めます。以下は\( H_6 \)までの変化のようすを表したものです。

スライダーで変化するものもつくってみました。以下\( n \)をずらして各自お楽しみください。
上のように定義される各\( H_n \)の共通部分
\( \displaystyle H=\bigcap_{n=0}^{\infty}H_n \)
を、ハルナック集合といいます。
このハルナック集合はなんと!先ほどのジョルダン測度の意味では面積を求めることができません。それを(直感的に)確認してみましょう。
ジョルダン測度では、内側から攻める内容量\( c(A) \)と外側から攻める外容量\( C(A) \)をそれぞれ考え、それらが一致している場合はその値を\( A \)の面積と考えるのでした。
ジョルダン内容量についてはどんな小さな\( \varepsilon \)を固定しても、一辺の長さが\( \varepsilon \)の面積がハルナック集合\( H \)の内部に含まれることができません。すなわち任意の\( \varepsilon \gt 0 \)で\( \displaystyle c_{\varepsilon}(A)=0 \)となりますからジョルダン内容量は
\( \displaystyle c(A)=0 \)
となります。
一方の外容量です。
\( H_1 \)は一辺\( \displaystyle \left(1-\frac{1}{4}\right)\frac{1}{2} \)の正方形が\( 4 \)個
\( H_2 \)は一辺\( \displaystyle \displaystyle \left( 1-\frac{1}{4}-\frac{2}{4^2}\right)\frac{1}{2^2} \)の正方形が\( 4^2 \)個
\( H_3 \)は一辺\( \displaystyle\left( 1-\frac{1}{4}-\frac{2}{4^2}-\frac{2^2}{4^3}\right)\frac{1}{2^3} \)の正方形が\( 4^3 \)個
含まれています。よって\( \displaystyle H_n \)には一辺の長さ
\( \displaystyle \left( 1-\frac{1}{4}-\frac{2}{4^2}-\frac{2^2}{4^3}-\cdots -\frac{2^{n-1}}{4^n}\right)\frac{1}{2^n} \)
\( \displaystyle\ \ =\left\{1-\frac{1}{4}\left(1+\frac{1}{2}+\left(\frac12\right)^2+\left(\frac12\right)^3+\cdots +\left(\frac12\right)^{n-1}\right)\right\}\frac{1}{2^n} \)
\( \displaystyle \ \ =\left\{1-\frac{1}{4}\frac{1-\left(\frac12\right)^n}{1-\frac{1}{2}}\right\}\frac{1}{2^n} =\frac{1}{2^{n+1}}\left(1+\left(\frac{1}{2}\right)^n \right) \)
の正方形が\( \displaystyle 4^n \)個含まれています。どんな風に\( \displaystyle H_n \)を覆うにしても上のような正方形たちは含まなければなりませんから、ジョルダン外容量について
\( \displaystyle \displaystyle C(H_n)\geq \left\{\frac{1}{2^{n+1}}\left(1+\left(\frac{1}{2}\right)^n\right)\right\}^2\times 4^n=\frac{1}{4}\left(1+\left(\frac12\right)^n\right)^2 \)
が成り立ちます。よって\( \displaystyle H=\bigcap_{n=0}^{\infty}H_n \)の外測度\( \displaystyle C(H) \)が\( \displaystyle \frac14 \)以上になるだろう、と推察することができます(下補足参照)。
したがってジョルダン内容量\( c(H) \)とジョルダン外容量\( \displaystyle C(H)\geq \frac14 \)が一致しませんから、ハルナック集合\( H \)はジョルダン可測ではないことがわかります。
(補足)上の推察部分は次のルベーグ測度の知識で正当化できます。\( \displaystyle H \)はジョルダン可測ではありませんが、”ルベーグ可測”で、ルベーグ測度とよばれる量\( m(H) \)は計算できます。このルベーグ測度については一般にジョルダン外測度以下、すなわち
\( \displaystyle C(H)\geq m(H) \)
であることが知られています。またルベーグ測度の諸定理から、この右辺について次のように極限操作が可能です。
\( \displaystyle m(H)=m\left(\bigcap_{n=1}^{\infty}H_n\right)\overset{\ast}{=}\lim_{n\to\infty}m(H_n) \)
\( \ \ \displaystyle =\lim_{n\to \infty}\frac{1}{4}\left(1+\left(\frac12\right)^n\right)^2=\frac14 \)
等式\( \ast \)で
「\( \displaystyle A_1\supset A_2\supset A_3\cdots \)かつ\( \displaystyle m(A_1)<\infty \)ならば
\( \displaystyle \lim_{n\to\infty}m(A_n)=m\left(\bigcap_{n=1}^{\infty}A_n\right) \)」
となることを使っています。
(補足ここまで)
今回はあまり触れることができませんでしたが、ルベーグ測度の定義はジョルダン測度よりもより図形を”柔軟に測定しやすい”ような定義になっており、これが結果的に測定可能な集合の範囲が増え、また極限操作に強い測度の構成に繋がっています。このへんの話はまたいつかやりたいと思います。
(参考)
新井仁之『ルベーグ積分講義』
今回はこの辺で。