今回の内容の動画版→曲率半径 〜曲線の曲がり具合を計算する〜
今回は、曲線の曲がり具合を円で近似する話です。
例として、曲線\( y=x^3 \)上の点\( (1,1) \)付近を円で近似してみましょう。
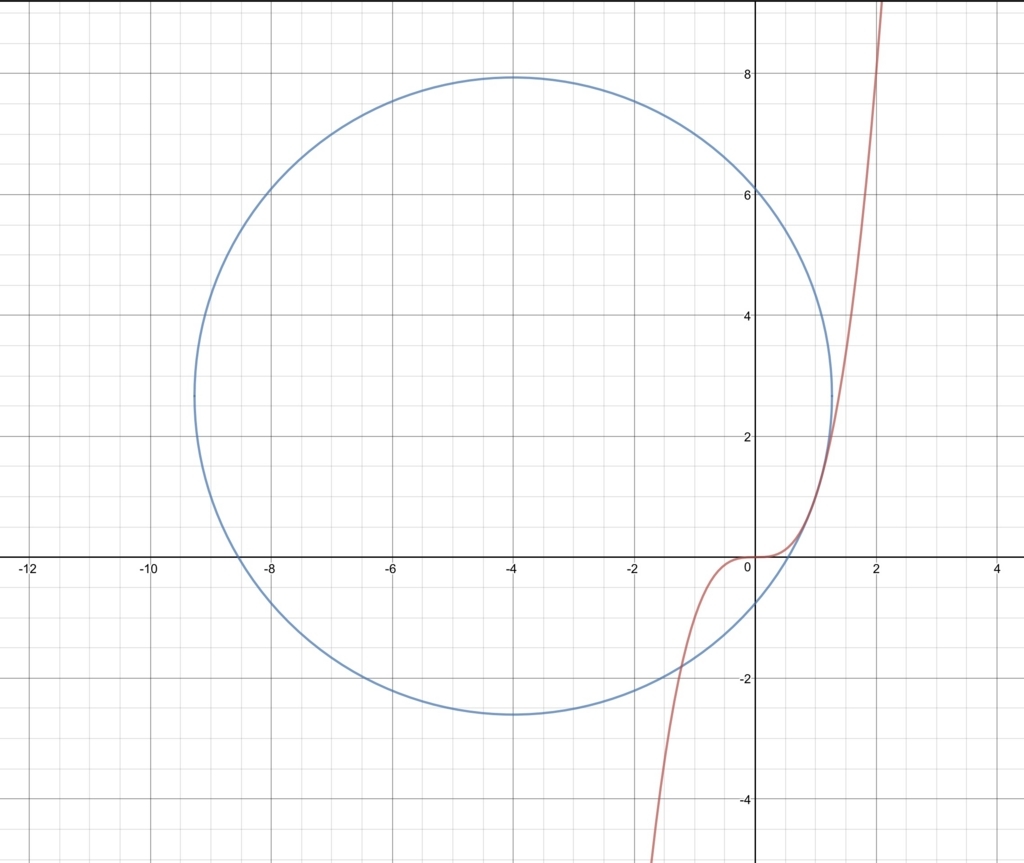
イメージとしては上の通り。赤の曲線を\( (1,1) \)付近で近似した、この青の円を計算して求めましょう。一般に円の方程式は中心\( (a,b) \)、半径\( R \)のとき
\( \displaystyle (x-a)^2+(y-b)^2=R^2 \)
として表すことができます。近似したい関数\( y=f(x) \)と”二階微分係数までが一致”という仮定を置くことで、次のように\( a,b,R \)を\( f(x) \)の情報で表すことができます。
[box class=”blue_box” title=”曲率中心、曲率半径”]\( y=f(x) \)を点\( (c,f(c)) \)上で近似する円の中心\( (a,b) \)、半径\( R \)は次のように計算できる(\( f^{\prime\prime}(c)\not=0 \)とする)。
\( \displaystyle a=c-\frac{1+f'(c)^2}{f^{\prime\prime}(c)}f'(c) \)
\( \displaystyle b=f(c)+\frac{1+f'(c)^2}{f^{\prime\prime}(c)} \)
\( \displaystyle R=\frac{(1+f'(c)^2)^{\frac32}}{|f^{\prime\prime}(c)|} \)
ただし、近似する円の上半分あるいは下半分を表す曲線を\( y=g(x) \)とするとき
\( \displaystyle f(c)=g(c), f'(c)=g'(c), f^{\prime\prime}(c)=g^{\prime\prime}(c) \)
が成り立っているものとする。なお、\( (a,b) \)を曲率中心、\( R \)を曲率半径、その逆数\( \displaystyle \frac{1}{R}\)を曲率という。
[/box] [box class=”glay_box” ](証明)
円の方程式
\( \displaystyle (x-a)^2+(y-b)^2=R^2 \)…⓪
を\( x \)で微分すると、
\( \displaystyle (x-a)+(y-b)y’=0 \)…①
となる。もう一度微分して
\( \displaystyle 1+y’^2+(y-b)y^{\prime\prime}=0 \)…②
となる(積の微分公式を使った)。
円の上半分あるいは下半分を表す曲線を\( y=g(x) \)とするとき,①、②へ\( x=c\)を代入して
\( \displaystyle (c-a)+(g(c)-b)g'(c)=0 \)…①’
\( \displaystyle 1+g'(c)^2+(g(c)-b)g^{\prime\prime}(c)=0 \)…②’
①’×\( g^{\prime\prime}(c) \)-②’×\( g'(c) \)により
\( \displaystyle (c-a)g^{\prime\prime}(c)-(1+g'(c)^2)g'(c)=0 \)
これを変形すると
\( \displaystyle a-c=-\frac{1+g'(c)^2}{g^{\prime\prime}(c)}g'(c) \)…(A)
となる。また、②’から
\( \displaystyle b-g(c)=\frac{1+g'(c)^2}{g^{\prime\prime}(c)} \)…(B)
となる。(A)、(B)と円の方程式⓪により、
\( \displaystyle R^2=(a-c)^2+(b-g(c))^2 \)
\( \displaystyle \ \ \ =\frac{1}{g^{\prime\prime}(c)^2}\left(1+g'(c)^2\right)^2(g'(c)^2+1)\)
\( \displaystyle \ \ \ =\frac{1}{g^{\prime\prime}(c)^2}\left(1+g'(c)^2\right)^3\)
すなわち
\( \displaystyle R=\frac{(1+g'(c))^{\frac32}}{g^{\prime\prime}(c)} \)…(C)
ここで、\( x=c \)においては
\( \displaystyle f(c)=g(c), f'(c)=g'(c), f^{\prime\prime}(c)=g^{\prime\prime}(c) \)
が成立していると仮定しているので、(A)〜(C)で\( g,g,g^{\prime\prime} \)をそれぞれ\( f,f’,f^{\prime\prime} \)に取り替えてよい。これで目標の式が導けた。(証明終)
[/box]さて、今求めた公式から、先ほどの\( f(x)=x^3 \)上の点\( (1,1) \)での曲率中心、曲率半径を計算してみましょう。
\( f'(x)=3x^2 , f^{\prime\prime}=6x\)であることから、曲率中心の座標は
\( \displaystyle a=1-\frac{1+3^2}{6}\cdot 3=-4 \)
\( \displaystyle b=1+\frac{1+3^2}{6}=\frac83 \)、
曲率半径は
\( \displaystyle R=\frac{(1+3^2)^{\frac32}}{|6|}=\frac{5\sqrt{10}}{3} \)
などと求まります。このようにして青色の円の情報が求められるのです。
ところで、曲率半径\( R \)は実は道路標識にも表示されていることがあります。高速道路で多いかも。
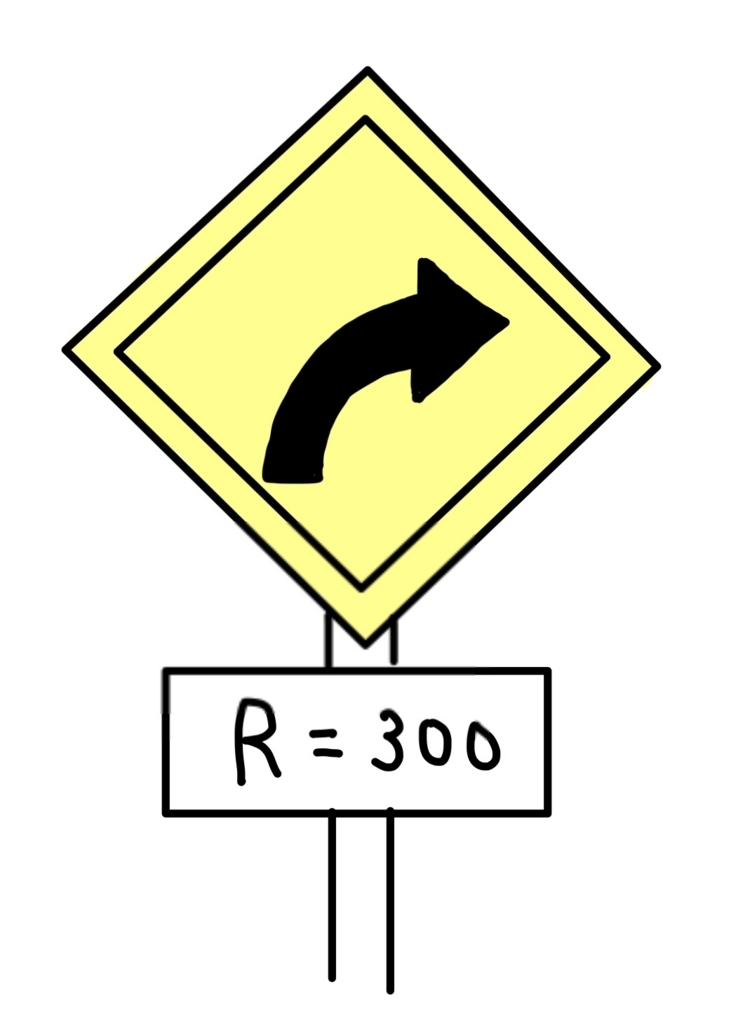
曲率半径\( R \)が小さいのは曲がり具合が急であることに対応します。上の道路標識は曲率半径Rが300mのカーブがこの先にあることを示しています。(私は車の運転をしないので実感としてはあまり分からないのですが、曲率半径が300mというのは結構きつめなカーブのようです)
では今回はこの辺で。
★★★
今回の内容の動画版です。