今回の内容を易しめにまとめた動画版→この机はいつのもの?【指数・対数関数の導入】
炭素14の話
炭素Cという元素の多くは原子量12、すなわち陽子とか中性子とかの粒が12個集まってできています。しかし、一定の割合(ウィキペディアによると0.00000000012%)で、14個の粒からなる炭素14という炭素も存在します。これは不安定な元素で、炭素14を集めたとき、\( T=\)5730)年ごとにそれらのうちの半分が別の物質に変化し、炭素14としては半分しか残らない、という性質があります(\( T \)を半減期といいます)。例えば1億個の炭素14を用意したら\( T= \)5730年後には5000万個しか残っておらず、それからさらに5730年後、つまり\( 2T=)2× 5730= \)11460年後には2500万個しか残らないのです。グラフにすると下のような感じ。
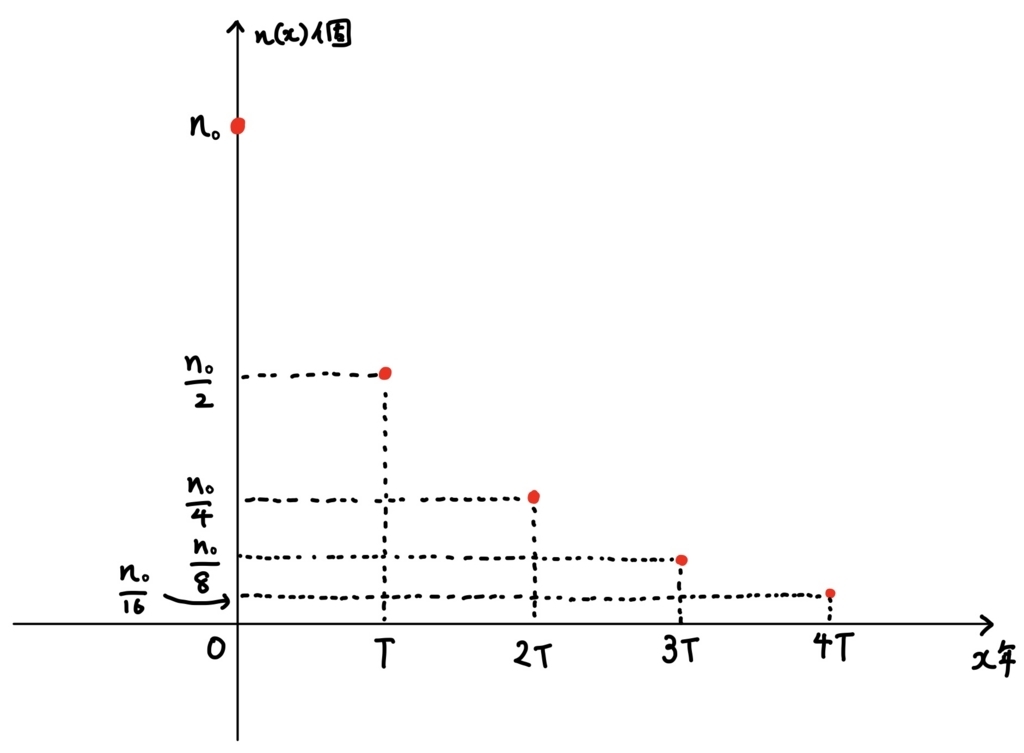
年代測定をするためには縦軸の値から横軸の値を求める必要があるので、この隙間をきちんと埋める必要があります。(でも、求める前から”指数関数感”がありありですね!)
炭素14の”生き残り率”\( g(x) \)の計算
さて、いくつか記号の準備を。\( n_0 \)は時刻\( t=0 \)での原子の個数、\( n(x) \)は\( x \)年経ったときの原子の個数を表すものとします。また、ある時点での原子の個数に対する、\( x \)年後に残っている原子の個数の比を\( g(x) \)とします。すなわち
\( \displaystyle g(x)=\frac{n(x)}{n_0} \)
と定義します。定め方から、
\( \displaystyle g(T)=\frac12, g(2T)=\frac14, g(3T)=\frac18 \cdots\) …(A)
が成立します。
この炭素14の”生き残り率”\( g(x) \)を求めたいのですが,(A)から
\( \displaystyle g(x)=\left(\frac12\right)^{\frac{x}{T}} \)
と予想するのは自然なことでしょう。(なお、この式はネイピア数\( e=2.71828… \)を使って\( g(x)=2^{-\frac{x}{T}}=e^{-\frac{x\log 2 }{T}} \)ともかけることに注意しておきましょう)。高校の授業では指数関数であることを認めてこの程度の導出でもよいと思われますが,そもそも指数関数かどうかを仮定せずに導くには、次のように\( g(x) \)の意味に立ち返って簡単な微分方程式を立てることになります。
[box class=”blue_box” title=” g(x) を求める”]半減期\( T \)の物質について、ある時点での原子の個数に対する\( x \)年後に残っている原子の個数の比を\( g(x) \)とおくと、
\( \displaystyle g(x)=e^{\frac{-x\log 2}{T}} \)…(⓪)
[/box] [box class=”glay_box” ](証明)簡単のため、\( g(x) \)は微分可能な関数として話を進める。
\( g(x) \)の意味から任意の\( x,x’ \)に対して
\( \displaystyle \frac{n(x+x’)}{n(x)}=g(x’) \)
が成り立つ(\( n(x) \)が初期の量であると考えればよい)。分母をはらうと
\( \displaystyle n(x+x’)=n(x)g(x’) \)…①
となる。
①の両辺を\( n_0 \)で割ると
\( \displaystyle g(x+x’)=g(x)g(x’) \)
となる。ここで\( \displaystyle f(x)=\log(g(x)) \)とおくと
\( \displaystyle f(x+x’)=\log(g(x+x’)) =\log(g(x)g(x’)) \)
\( \displaystyle \ \ =\log(g(x))+\log(g(x’))=f(x)+f(x’) \)
となる。\( x’\to 0 \)として\( f(0)=0 \)となる。また、極限の定義により
\( \displaystyle f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\)
\( \displaystyle \ \ =\lim_{h\to 0}\frac{f(x)+f(h)-f(x)}{h}\)
\( \displaystyle \ \ =\lim_{h\to 0}\frac{f(h)}{h}=\lim_{h\to 0}\frac{f(h)-f(0)}{h-0}\)
\( \displaystyle \ \ =f'(0) \)(一定)
となる。よってある定数\( a \)が存在して\( f(x)=ax \)すなわち、
\( \displaystyle \log(g(x))=ax \)…②
と表される。\( a \)については②の両辺に\( x=T \)を代入すると
\( \displaystyle \log \frac12=aT \)
から\( a=\frac{-\log 2}{T} \)と定まる。最後に、②を書き換えれば
\( \displaystyle g(x)=e^{ax}=e^{\frac{-x\log 2}{T}} \)
となって結論の式(⓪)を得る。(終)
[/box]年代測定の計算を実際にやってみる
ここで年代測定法の前提となる補足をしておきます。半減期があるため、地球上に存在する炭素14の割合は十分時間が経つことで0に近づくはずですが、実際にはどの時代もほぼ一定の割合存在しています。実はこれは、大気の上層部で宇宙線の影響で炭素14が作られており、それが酸素と結合して二酸化炭素の姿をして地表に降りてくるのからなのです。炭素14の作られる量と、半減期で減る量とが釣り合っているため、地球上の大気(そしてそれを吸う植物、それを食べる動物や人間も!)の中に存在する炭素14の割合はほぼ一定なのです。しかし、動物が死んだ瞬間、あるいは木が切られた瞬間に、大気等から体内に供給されていた炭素14の補充が終了し、炭素14の減少がはじまります。歴史的な建造物や作品に対して、この炭素14の減少ぐあいを測定して年代を推定しようというのが年代測定法のアイディアとなります(炭素12の量と炭素14の量の比に注目するようですが、本質的には同じことなので、以下簡単のため炭素14の量に着目することにします)。
さて、現在生きている木の炭素14の量、測定したい歴史的なモノの炭素14の量をそれぞれ\( N,N’ \)とします。半減期の定義から、
\( \displaystyle \frac{N’}{N}=\frac12 \)
となっているときは作られてから\( T=5730 \)年ほど経過したことを表し、また
\( \displaystyle \frac{N’}{N}=\frac14 \)
となっているときは作られてから\( 2T=11460 \)年ほど経過したことを表します。
しかし実際には\( \frac{N’}{N} \)が\( \frac{1}{2^n} \)の形をしているというのはあまりないことでしょう。ここで導出した式(⓪)が活躍します。
例えば測定の結果が\( \frac{N’}{N}=\frac{10}{11} \)であるとき、(⓪)より
\( \displaystyle e^{\frac{x\log 2}{T}}=\frac{10}{11} \)
すなわち
\( \displaystyle x=-\frac{T\log(10/11)}{\log 2} \)
となります。\( \displaystyle T=5730, \log 2=0.7, \log(10/11)=-0.1 \)として計算するとほぼ
\( \displaystyle x=819 \)
となります。つまり、約800年前のモノだろうと推定できるわけです。
以下、年代測定法に関しての歴史小話を1つ。
5世紀半ば、アングロ=サクソンのイングランド侵入に抵抗した、アーサー王という英雄がいました。彼に関する『アーサー王物語』の挿絵の中に、アーサー王に仕える騎士たちが集うときに使用した円卓のテーブルが描かれています。この円卓とされるものが、ウィンチェスター城というイングランド南部の城にあるのですが、本当にアーサー王の時代のものなのかがよく分かっていませんでした。そこで、1976年に、その円卓に含まれる炭素14の量\( N’ \)および同じ材質の生きている木の炭素14の量\( N \)を測定したところ、およそ\( \frac{N’}{N}=\frac{10}{11} \)となりました。上の計算の通り、円卓は800年ほど前のものであるという判定になり、アーサー王が生きていた時代(1500年以上前)のものではないだろうという結論になったそうです。残念!
では、今回はこの辺で。
★★★
今回の内容をテーマにした動画です。