今回は統計で登場する、チェビシェフの定理(あるいはチェビシェフの不等式)について扱います。データは離散量として考えます。
[box class=”blue_box” title=”チェビシェフの定理”]平均値が\( \mu \)、標準偏差が\( \sigma \)の分布があったとする。任意の正数\( k \)に対し、”平均\( \mu \)からの距離が\( k\sigma \)”より小さいデータ、すなわち
\( \displaystyle \ \ \mu-k\sigma <x_i<\mu +k\sigma \)
を満たすデータ\( x_i \)の度数の和は、全度数の\( \displaystyle 1-\frac{1}{k^2} \)以上ある。
[/box]文字だらけでよく意味が掴みにくいので、例えば\( k=2 \)としてみましょう。すると、平均\( \mu \)からの距離が「標準偏差\( \sigma \)」の2つ分より小さいデータが全体の75%以上あることを主張しています。そして定理のスゴイところは、どんな分布でもこれが成り立つという点です。自分でどんなにテキトーに分布を作っても、平均\( \mu \)からの距離が「標準偏差\( \sigma \)」の2つ分より小さいデータが全体の75%以上あるのです(大事なことなので2回いいました)。以下よく使うフレーズなので、「平均\( \mu \)からの距離が標準偏差\( \sigma \)の2つ分より小さい範囲」のことを2シグマ範囲と呼ぶことにします。
では、ちょっと具体例を持ってきます。
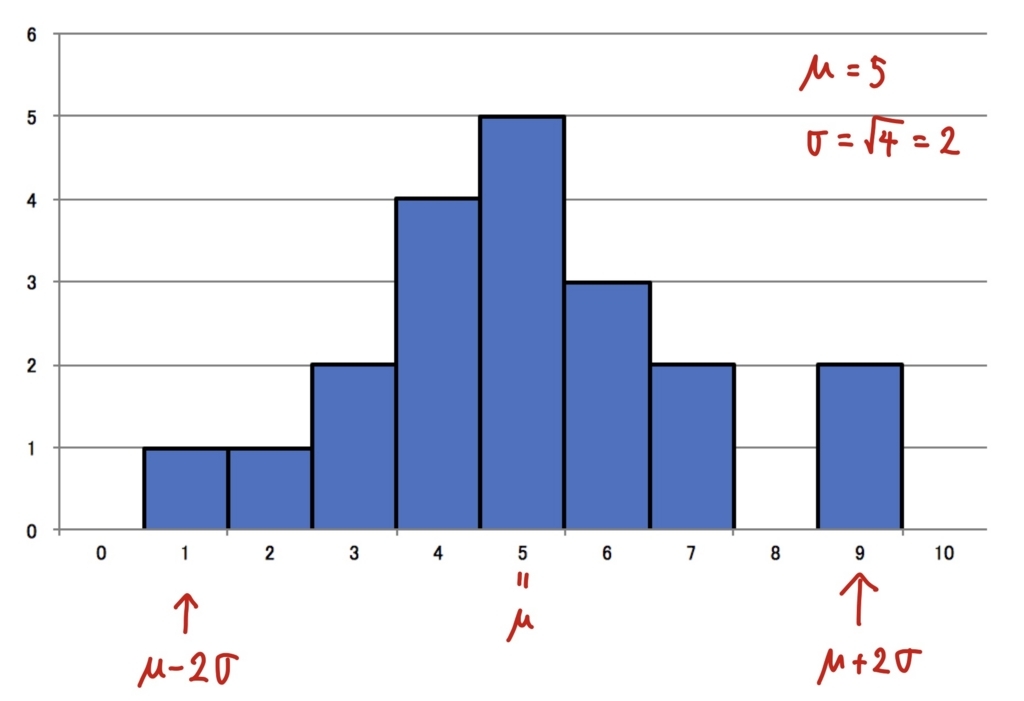
上の分布は、変量\( x_i=i \ (0\leq i\leq 10)\) に対してそれぞれの度数\( f_i \)が0,1,1,2,4,5,3,2,0,2,0で、平均\( \mu=5 \)、標準偏差はぴったり\( \sigma=2 \)となっています(\( \mu, \sigma \)が簡単になるようにデータを作りました)。
さて、上の分布で2シグマ範囲(平均\( \mu \)からの距離が標準偏差\( \sigma \)2つ分より小さい範囲)にあるデータの度数の和は\( f_2+f_3+\cdots f_8 =17 \)であり、全体の17/20=85%ということになります。
データ数20,平均5で変量が0〜10の範囲で、もう少し2シグマ範囲のデータを減らせないかと(人工的に)作ってみたのが次の分布です。
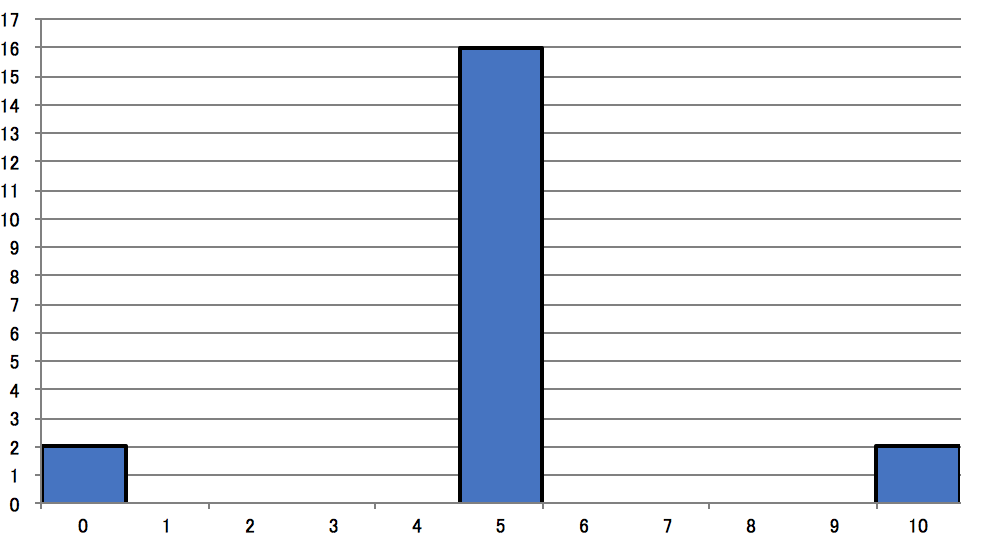
平均\( \mu=5 \)、標準偏差\( \sigma=\sqrt5 \)で2シグマ範囲\( (5-2\sqrt5, 5+2\sqrt5)=(0.53, 9.47) \)内のデータの割合は\( 16/20=80 \) %です。
(理論的な限界の75%に近いものを作るには、もっとデータ数を増やす必要がありそう…後日やる)
では定理の証明に移ります。分散の定義の和を”\( k \)シグマ範囲”の内側・外側に分けて評価していきます。
[box class=”blue_box” title=”チェビシェフの定理(再掲)”]平均値が\( \mu \)、標準偏差が\( \sigma \)の分布があったとする。任意の正数\( k \)に対し”\( k\)シグマ範囲”にあるデータ、すなわち
\( \displaystyle \mu-k\sigma<x_i<\mu +k\sigma \)
を満たすデータ\( x_i \)の度数の和は、全度数の\( \displaystyle 1-\frac{1}{k^2} \)以上ある。
[/box] [box class=”glay_box” ](証明)
データ数を\( N \)、各変量\( x_i \)の度数を\( f_i \)とする。分散の定義
\( \displaystyle \sigma^2=\frac{1}{N}\sum (x_i-\mu)^2f_i \)
を2つの和に分ける。
\( \displaystyle \sigma^2=\frac{1}{N}\sum (x_i-\mu)^2f_i \)
\( \displaystyle =\frac{1}{N}\sum_{\mbox{内側}}(x_i-\mu)^2f_i+\frac{1}{N}\sum_{\mbox{外側}}(x_i-\mu)^2f_i \)
ここで内側とは \( \displaystyle \mu-k\sigma<x_i<\mu +k\sigma \)を満たす\( x_i \)についての和で、外側とは\( \displaystyle x_i\leq \mu-k\sigma \)または\( \displaystyle \mu+k\sigma \leq x_i \)を満たす\( x_i \)についての和を表すものとする。
ここで”太っ腹に”内側のデータを捨て、区間外のデータについては\( \displaystyle (x_i-\mu)^2\geq (k\sigma)^2 \)であることを使うと、
\( \displaystyle \sigma^2 \geq \frac{1}{N}\sum_{\mbox{外側}}(x_i-\mu)^2f_i\)
\( \displaystyle \ \ \ \geq \frac{1}{N}\sum_{\mbox{外側}}(k\sigma)^2f_i=k^2\sigma^2\frac{1}{N}\sum_{\mbox{外側}}f_i \)
すなわち
\( \displaystyle \frac{1}{N}\sum_{\mbox{外側}}f_i \leq \frac{1}{k^2} \)
となる。外側のデータの割合が\( \displaystyle \frac{1}{k^2} \)以下ということなので、内側のデータの割合は\( \displaystyle 1-\frac{1}{k^2} \)以上、すなわち
\( \displaystyle\frac{1}{N}\sum_{\mbox{内側}}f_i \geq 1-\frac{1}{k^2} \)
が成立する。(証明終)
[/box]なお、データ作成時に、以前公開したエクセルファイルを使っています。簡単に度数分布表を作ることができますので興味のある方はチェックを。
[kanren postid=”128″]では今回はこの辺で。
(参考文献) 平均値の統計 (数学ワンポイント双書 35)
