今回の内容の動画版→平面グラフには次数が5以下の点が必ずある
平面グラフの話題です。以前の記事で、平面グラフの定義について述べた後、オイラーの公式の証明を行いました。
[box class=”blue_box” title=”平面グラフに関するオイラーの公式”]平面グラフの頂点数を\( v \)、辺数を\( e \)、面数\( f \)をとすると、次が成り立つ。
\(\ \ \displaystyle v-e+f=2 \)
[/box]この定理の証明自体もなかなか面白いです。興味のある方は是非ご覧ください。
一応、この記事から読む方向けに平面グラフの最低限の知識を言っておくと、平面グラフってのは頂点と辺からなるグラフで、辺が交差せず、多重辺も存在しないものです。例えばこんな感じ↓
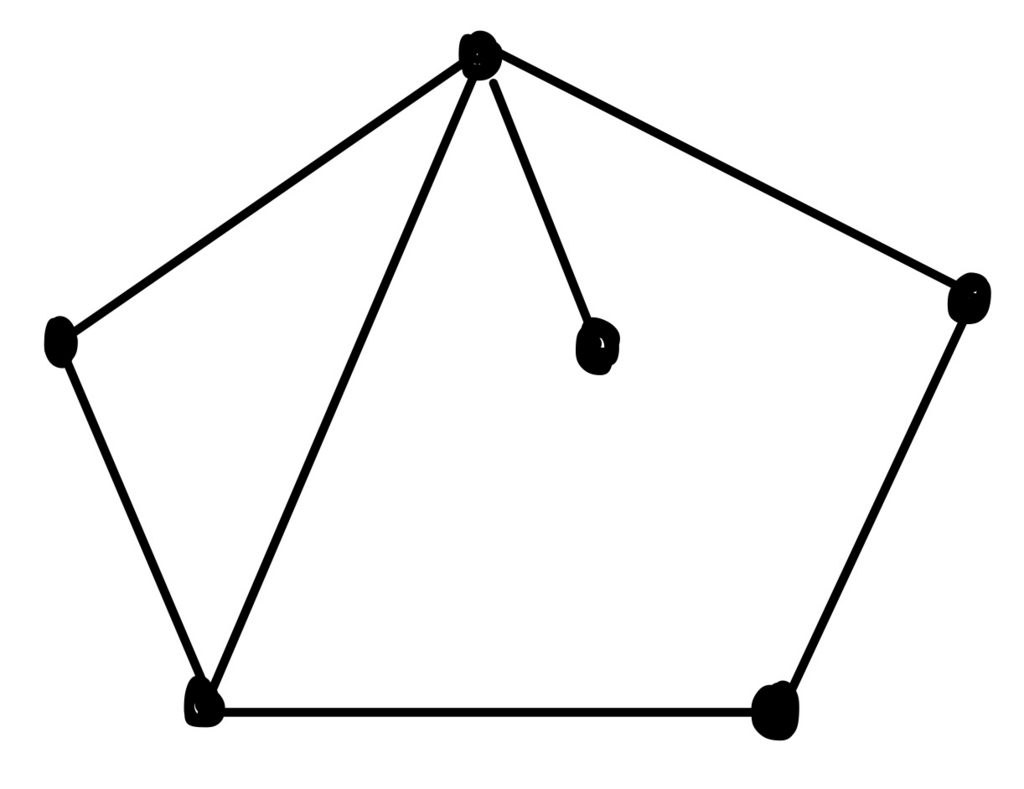
辺が交差していたり、多重辺があるものは平面グラフとはいいません。
さて、今回はオイラーの公式を利用して、平面グラフの最低次数に関する定理を証明します。なお次数とは頂点を端にもつ辺の個数のことで、要するに”頂点からでている辺数”を表します。頂点\( x \)の次数を記号\( \deg (x)\)と表します。例えば次の図をご覧ください。
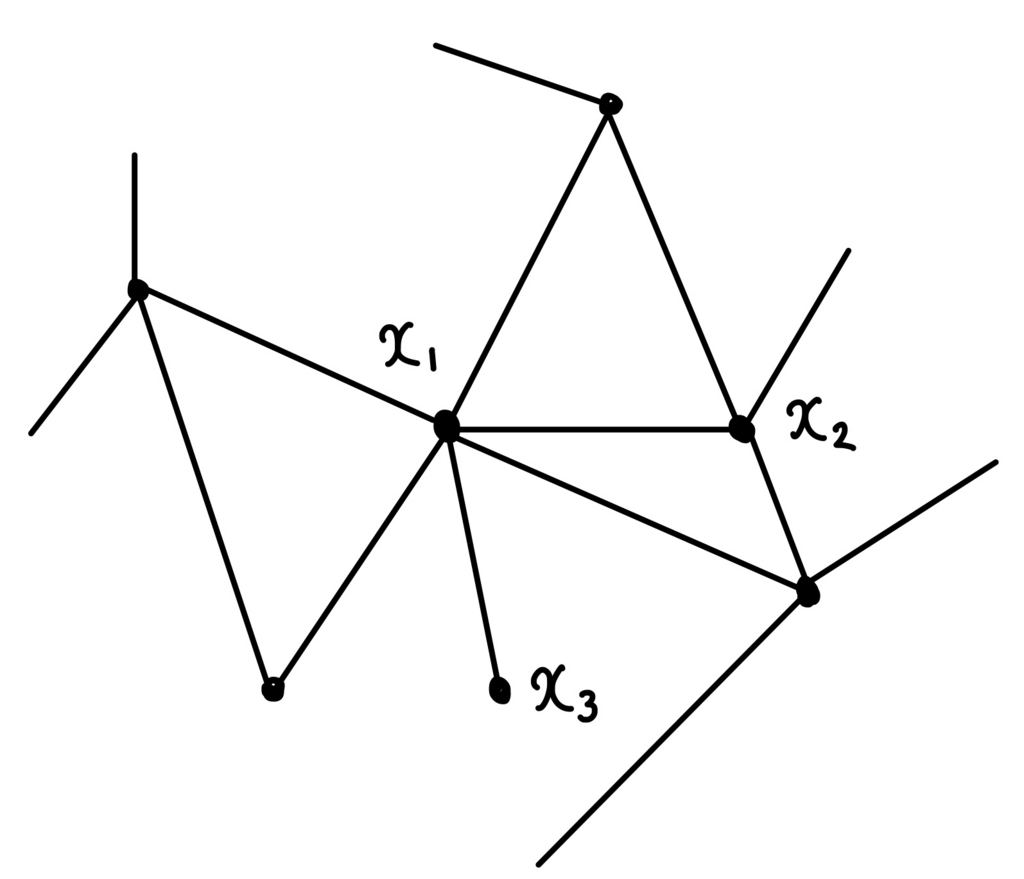
上図の頂点\( x_1, x_2, x_3 \)の次数はそれぞれ\( 6,4,1\)です。記号で表すと
\( \displaystyle \deg (x_1)=6, \deg (x_2)=4, \deg (x_3)=1 \)
となります。
さて、平面グラフは多重辺や交差の条件さえ守ればいくらでも複雑なものを作ることができるので、どの頂点も次数が10以上とか、どの頂点も次数が100以上とか、最低次数が大きいグラフがかけそうな気がします。しかし実は「どんなに複雑に平面グラフを書いても、次数が5以下の頂点がある」ことが知られています。
[box class=”blue_box” title=”平面グラフの最低次数”]平面グラフには次数が5以下の頂点が存在する。
[/box]
では、上の定理の証明のために、平面グラフの辺数\( e \)を上から評価する次の補題を示します。
[box class=”blue_box” title=”補題”]頂点数3以上の平面グラフにおいては
\( \displaystyle e\leq 3v-6 \)…(A)
が成立する。
[/box] [box class=”glay_box” ](証明)
平面グラフ\( G \)の各辺の両側に小石を1個ずつ置いたところを想像してほしい。
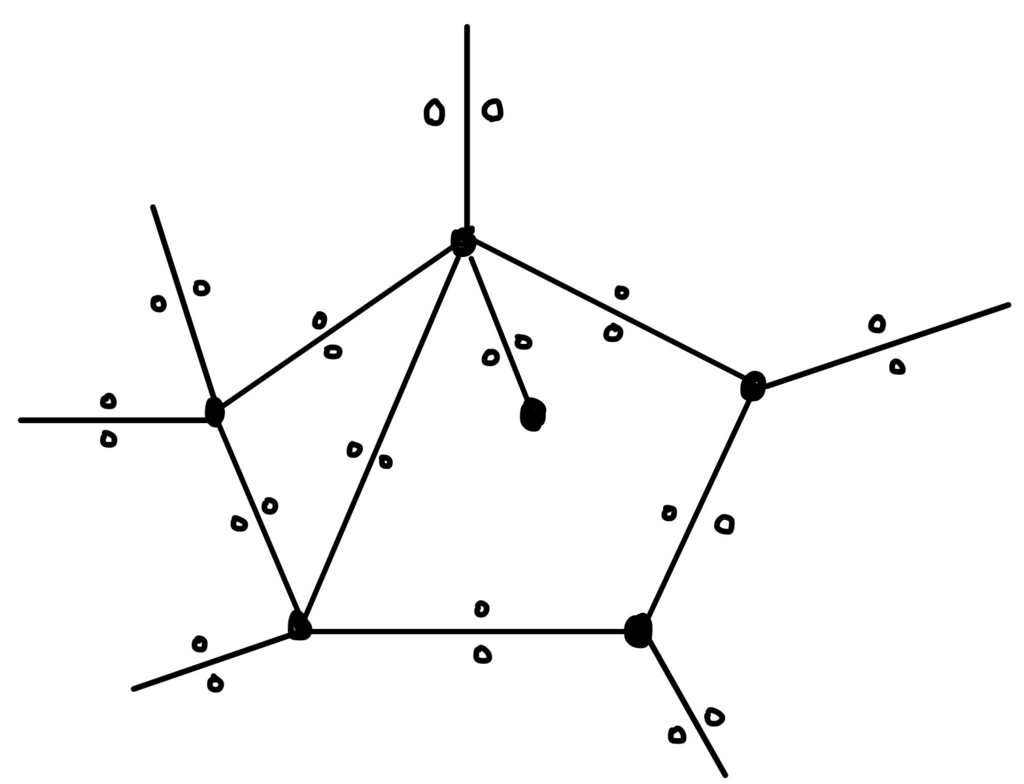
面は少なくとも3つの辺で囲まれるので、どの面にも3個以上の小石が配置されることになる。すなわち
\( \displaystyle \ \ 2e\geq 3f \)…①
が成り立つ。一方オイラーの公式を3倍すると
\( \displaystyle \ \ 3v-3e+3f=6 \)…②
となる。①と②から
\( \displaystyle \ \ 3v-3e+2e\geq 6 \)
すなわち
\( \displaystyle \ \ 3v-6\geq e \)
で(A)が成り立つ。(証明終)
[/box]では、目標の証明に移ります。
[box class=”blue_box” title=”平面グラフの最低次数(再掲)”]平面グラフには次数が5以下の頂点が存在する。
[/box]
[box class=”glay_box” ]
(証明)一般に、各頂点\( x \)の次数\( \deg (x) \)の和について
\( \displaystyle \sum \deg (x)=2e \)…③
が成り立つことに注意しよう(「握手補題」と呼ばれる)。これは上の議論と同様に各辺に対して辺をまたぐように2個ずつ小石を置いたとき、
・小石の個数=頂点の次数の和
であり、また
・小石の個数=辺数の2倍
でもあることからわかる。
では、定理の証明に移ろう。すべての頂点の次数\( \deg (x) \)が6以上となるような平面グラフが存在したとすると、③(握手補題)により
\( \displaystyle 2e=\sum \deg(x)\geq 6v \)
すなわち
\( \displaystyle e\geq 3v \)
と\( e \)の下からの評価が成り立つ。補題で証明した\( e \)を上から評価する式(A)と組み合わせると、
\( \displaystyle \ \ 3v\leq e\leq 3v-6 \)
となり矛盾が生じる。よってすべての頂点の次数が6以上の平面グラフは存在しない。(証明終)
[/box]論理で存在が証明できるのは数学の強さを感じますね!
なお、最低次数が5のグラフとしては次のような例があるので、定理の主張を強めて”次数を4以下”にすることはできません。
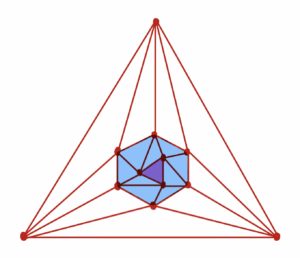
色はなんとなく塗ったものです。三角形の中に六角形、六角形の中に三角形がある形です(YouTubeのコメント欄にて教えてもらいました)
では今回はこの辺で。
★★★
今回の内容の動画版