今回の内容の動画版です→ピックの定理
ピックの定理は、頂点が格子点上にある多角形(格子多角形)の面積を簡単に求めることができる公式です。
[box class=”blue_box” title=”ピックの定理”]点がすべて格子点上にある多角形の面積\( S \)は次のように計算できる。ただし内部の格子点の数を\( i \)、辺上の格子点の数を\( e \)とする。
\( \displaystyle S=i+\frac{e}{2}-1 \)
[/box]
ピックの定理は初めてだ、という方は是非下の例で確認してみてください。まず図形を適当に三角形や四角形に分割して計算してみましょう。
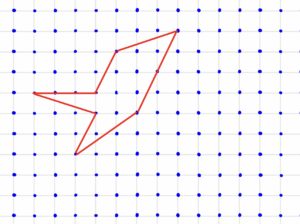
↓(適当な分割で面積を出す)
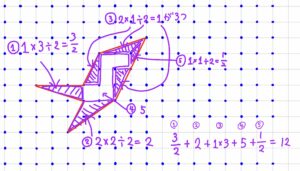
分割された三角形や四角形の面積の合計として、図形の面積が12と計算できますね。実はこの面積12というのは、内側の格子点の数\( i=8 \)、辺上の格子点の数\( e=10 \)を使って
\( \displaystyle \ \ S=8+\frac{10}{2}-1=12 \)
とピックの定理からも計算ができます(下図参照)。
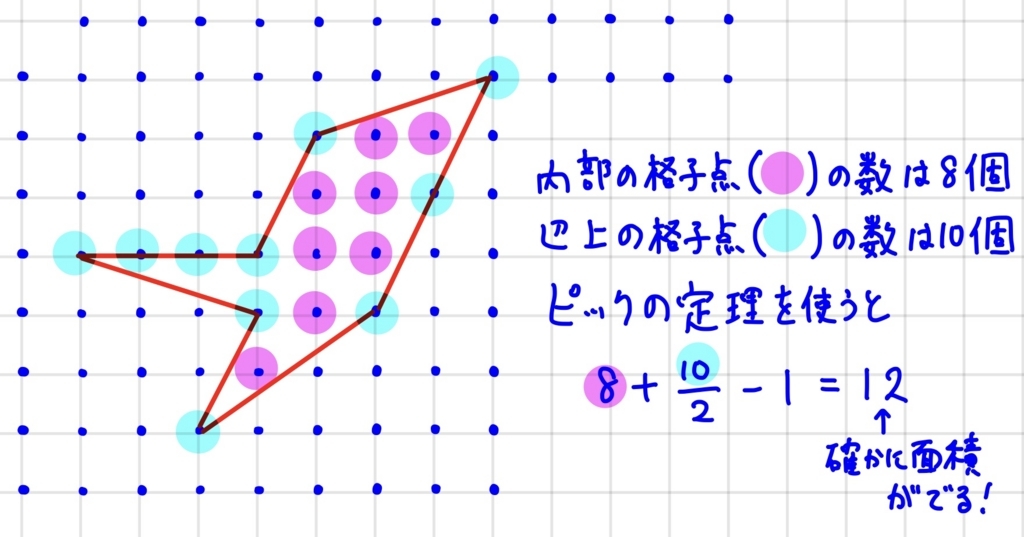
今回はこの定理がなぜ成り立つのかを説明してみようと思います。定理自体も驚きなのですが、今回の証明方法自体にも驚いてしまうかもしれません。
[box class=”glay_box” ](証明)
平面図形についての話ではあるが、立体的な視点で考察する。
目の前に無限に広がる格子点つきのテーブルがあり、そのテーブルに考えている多角形が描かれているとしよう。体積がちょうど1の水をいれたコップを用意し、各格子点の上に逆さまに配置する。コップの口は円で、その円の中心が格子点と重なるようにしている。
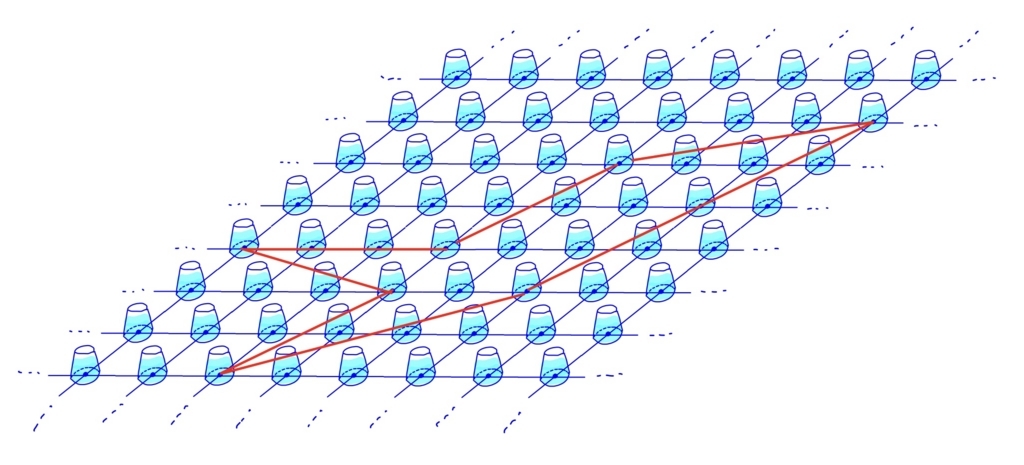
この状態で、すべてのコップを一斉に真上へ持ち上げる。各コップ内にあった水は一瞬だけその格子点の付近にあるが、しばらくすると無限に広がるテーブルを覆う。各格子点につき体積1の水を供給しているため、張っている水の高さは1となる。
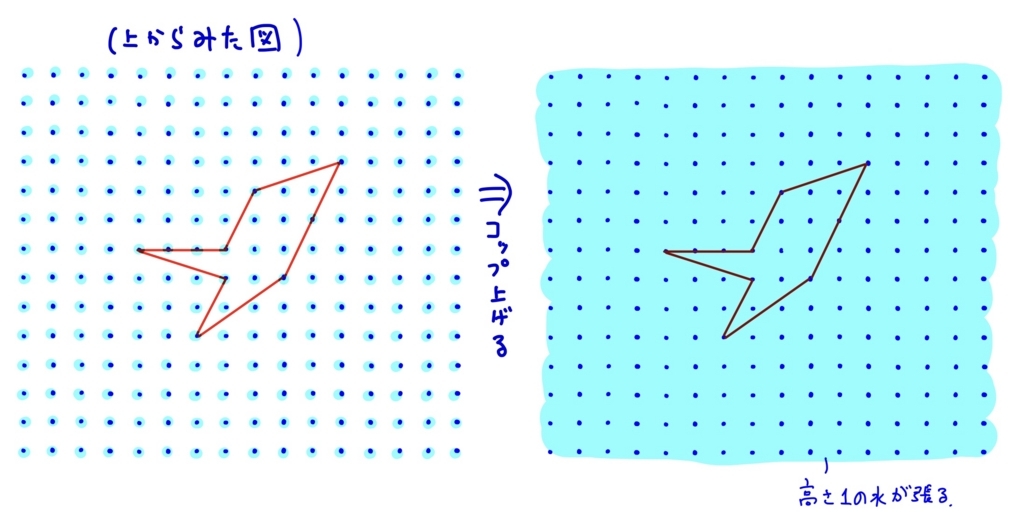
高さが1なので、水を張った後に図形の上にある水の量が、今求めたい図形の面積\( S \)と等しい。そしてその水の量というのは、
「コップを上げる前に、多角形の内部の上にある水の量」
と等しい(理由はすぐ後で説明する)。
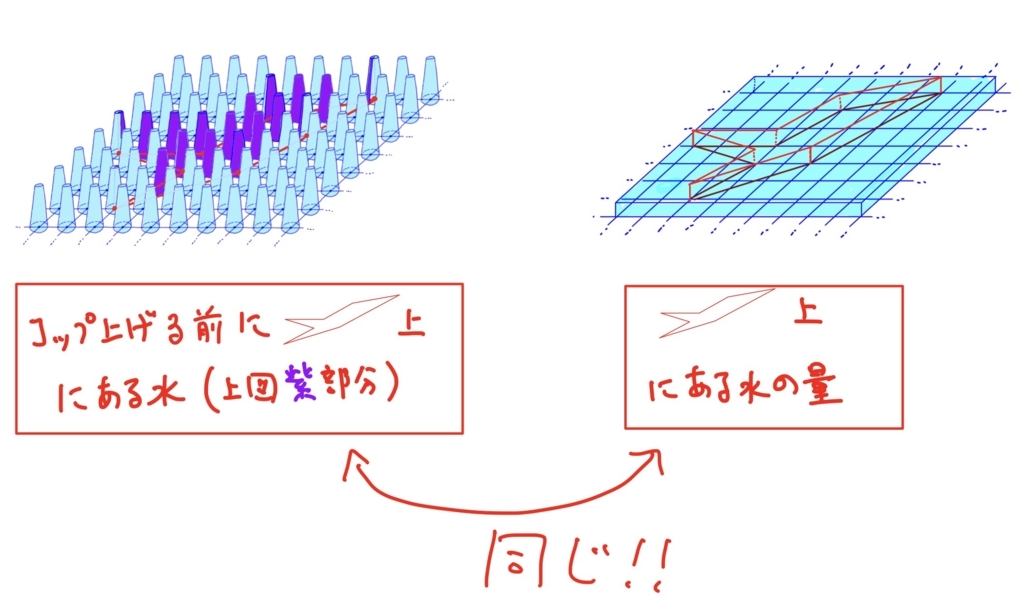
(「コップを上げる前に、多角形の内部の上にある水の量」というのがわかりにくい方は、一時的にコップ内の水をゼリーのようなものと考え、コップをあげて(水ではないので流れずそのままの形で残り)、多角形の形に沿ってテーブルの真上から垂直に包丁をいれたときの、多角形の内部の上に乗っかっているゼリーの量、と考えるとよいかも。)
コップをあげる前後で図形上の水の量が同じというのは次のように考えればよい。任意の辺について、辺をまたぐ水の移動を考えよう。コップを上げてから、時間がたって水が水平に張るまでの間に、辺をまたいで水の移動が当然発生する。しかし、どの辺について考えても、その辺の中心に関して点対称に格子点が分布している。よってその対称性から、辺をまたいだ水の出る量と入る量は等しいと考えられる。コップの水を供給した後、多角形の内部から辺をまたいで外に水が出てしまっても、同じ量の水が辺をまたいで入ってくるのである。
以下、「コップを上げる前に多角形の内部の上にある水の量」(これが求めたい面積\( S \)となる)を求めよう。
多角形の内部の上に水があるようなコップは、次の3つに分類される。
①コップの水がすべて多角形の内部の上にあるもの
②コップの水の一部が多角形の内部の上にあり、対応する格子点が頂点ではないもの
③コップの水の一部が多角形の内部の上にあり、対応する格子点が頂点であるもの
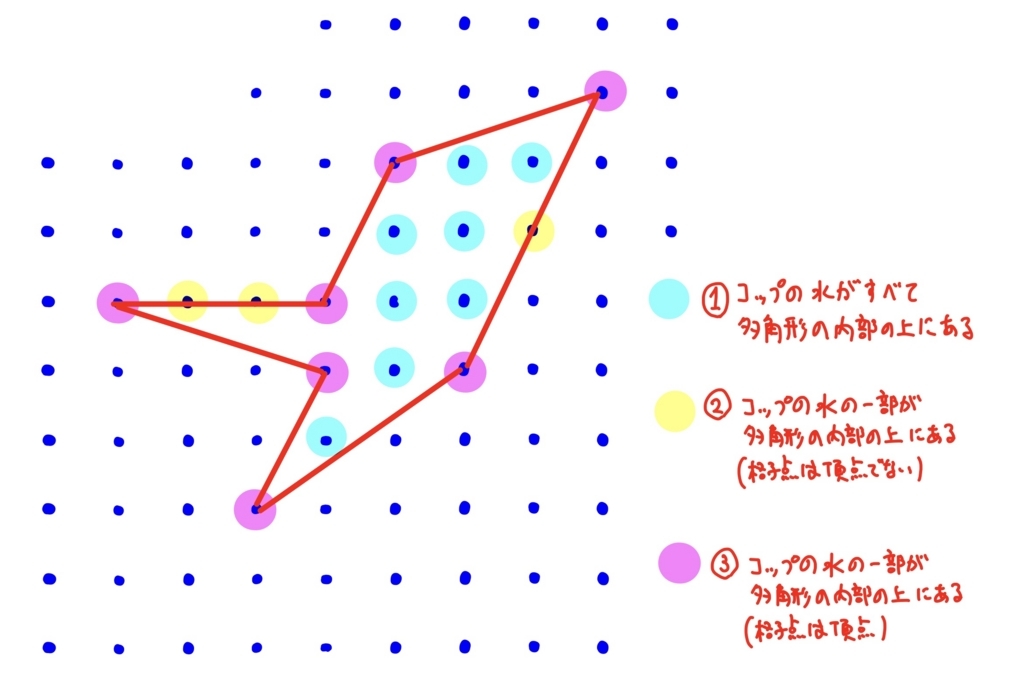
では、上の①〜③のコップ内にある水のうち、多角形の内部の上にある水の量の合計(=多角形の面積\( S \))を計算しよう。
①のコップはコップ内のすべての水が多角形の内部の上にあるのでそのコップの個数がそのまま面積に寄与する。…(A)
②のコップはコップ内のちょうど半分が多角形の内部の上にあるのでコップの個数の半分が面積に寄与する。…(B)
最後に③について。③のコップの個数を\( n \)とし、各内角の大きさを\( \displaystyle \theta_1, \theta_2, \cdots , \theta_n \)とする。
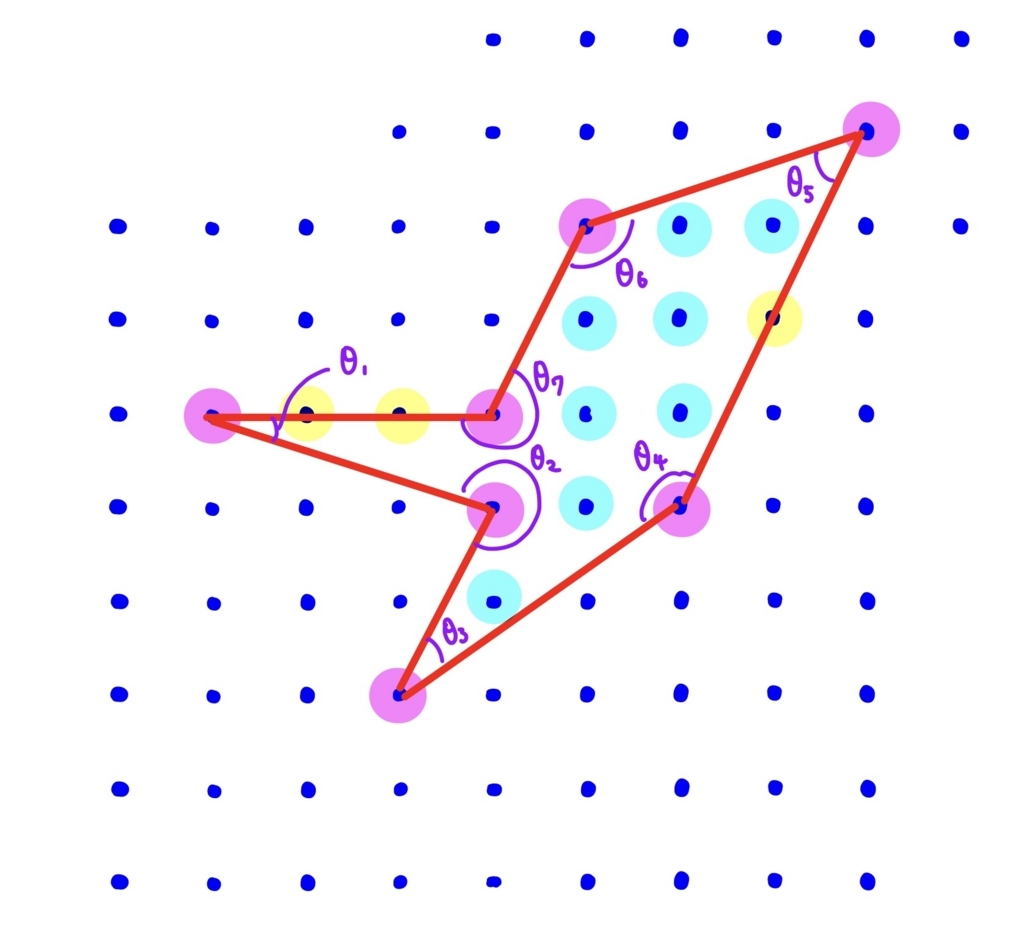
\( \theta_i \)に対応する格子点について、そのコップの内部の水のうち多角形の内部の上にある水の量は
\( \displaystyle 1\times \frac{\theta_i}{2\pi}=\frac{\theta_i}{2\pi} \)
である。これらを合計しよう。\( n \)角形の内角の和が\( \pi(n-2) \)であることを思い出すと、
\( \displaystyle \sum_{i=1}^{n}\frac{\theta_i}{2\pi}=\frac{n-2}{2}=\frac{n}{2}-1 \)…(C)
となる。右辺は(③のコップの数の半分)\( -1 \)となっていることに気をつけよう。
(A)、(B)、(C)の結果を総合すると、求める水の量(=多角形の面積\( S \))は
\( S= \)(①のコップの数)+(②のコップの数の半分)+(③のコップの数の半分)\( -1\)
であり、
・(①のコップの数)\( =i \)
・(②のコップの数)+(③のコップの数)\( =e \)
と合わせて書き換えると
\( \displaystyle S=i+\frac{e}{2}-1 \)
を得る。(証明終)
[/box]多角形を三角形に分割して計算する証明がオーソドックスのようですが、場合分けが多く発生してあまり好きになれませんでした。こちらのコップの水を張る証明ですと、証明の手順から公式の形が思い出しやすいですし、面白い!
では今回はこの辺で。
(参考)
時枝正, 数学セミナーの2014年7月号記事「物理を数学へ応用する」
★★★
今回の内容の動画版です↓
