【四色定理】地図は４色で塗り分けられる【四色問題】

今回の内容の動画版→【四色問題】どんな地図でも４色で塗り分け可能 

今回は「四色定理」という地図の塗り分けに関する話題です。塗り分けということなので、辺で接している領域は違う色で塗る、というルールで塗ります。以下に２つ例を示します。

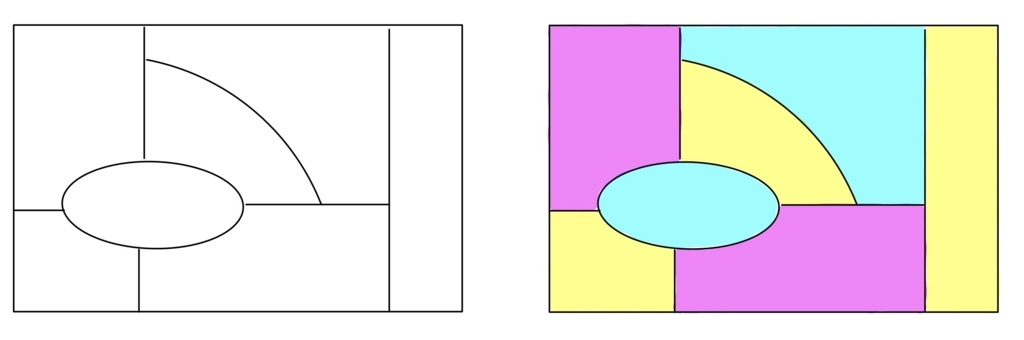
上の例だと3色(青、黄色、赤)で塗り分けられています。

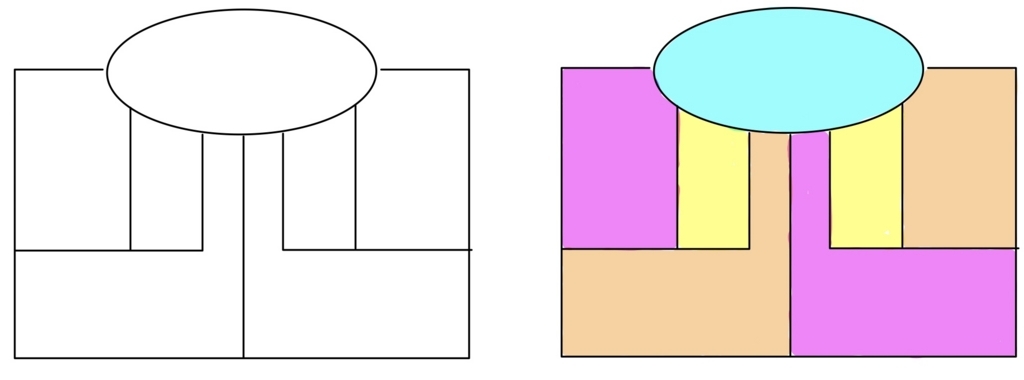
上の例だとちょっと複雑になっていて4色(青、黄色、赤、肌色)なければ塗り分けができません。

さて、地図というのはいくらでも複雑なものを作ることができますから、その複雑さに応じて、塗り分けのためにたくさんの色が必要になりそうな気がします。しかしその直感に反して、実は４色あれば十分である、ということが知られています。これが四色定理と呼ばれる数学的事実で、アッペルとハーケンによって1976年に証明されました。

４色定理は、通常平面グラフによって考察されることが多いです。いま、地図上の領域の大きさや形は塗り分けの話には関係がなく、各領域が接している・接していないという情報だけが必要です。ということで、各領域を頂点、接している領域同士を辺で結ぶ、という約束でどんな地図でも平面グラフに書き換えられます。つまり、地図の塗りわけ問題は、平面グラフを考察すれば良いのです。

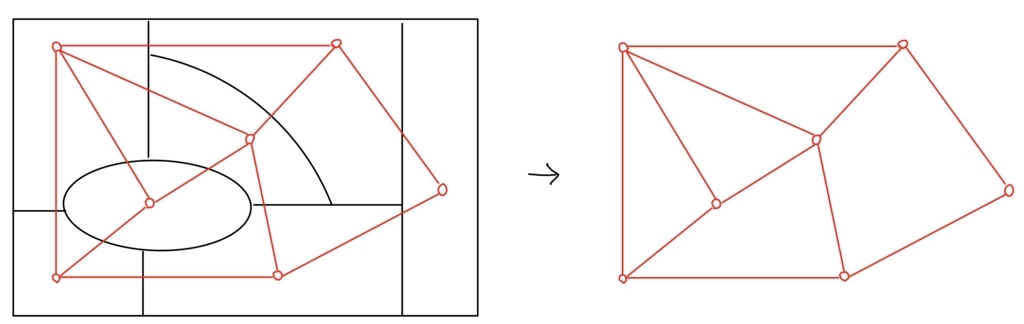
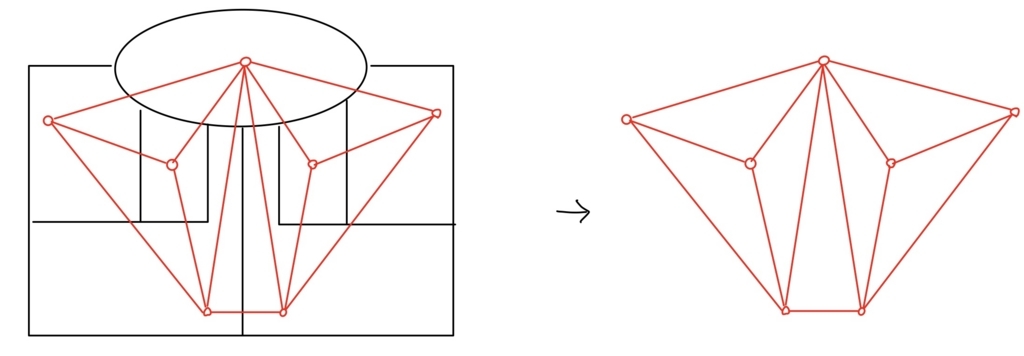
平面グラフ\(  G \)の頂点に、隣接する頂点の色は異なるように、色をつけることを彩色といい、グラフ\(  G \)が\(  n \)色以下で彩色できるとき、グラフ\(  G \)は\(  n- \)彩色可能であるといいます。平面グラフの彩色が地図の塗り分けに対応しているわけですね。

平面グラフの言葉を使うと、四色定理は次のように述べることができます。

任意の平面グラフは\(  4- \)彩色可能である。
[/box]

四色定理の証明は、場合分けをめちゃめちゃたくさんやってコンピュータを援用するというスタイルのようです。現在でもエレガントに証明する方法は(おそらく)見つかっていないようなので、今回は四色定理の証明をするのではなく、少し妥協して、"五色定理"を証明しようと思います。五色定理の証明には、任意の平面グラフには次数が5以下の頂点が存在する、という事実を使います。このことについては以下の記事をご覧ください。

では、五色定理の証明に移りましょう。

任意の平面グラフは\(  5- \)彩色可能である。

(証明)

平面グラフ\(  G \)に対し、頂点数\(  n \)に対する帰納法を使う。頂点数が\(  5 \)以下の場合には各頂点に違う色をそれぞれ塗ることで\(   5-\)彩色可能であることがわかる。頂点数が\(  n-1 \)以下のときに定理が成り立つとする。平面グラフには次数が5以下の頂点\(  x \)が存在する。帰納法の仮定により、\(  G \)から頂点\(  x \)(とそれに隣接する辺)を取り除いたグラフ\(  G-x \)は\(  5- \)彩色可能である。もし\(  x \)の次数が4以下であれば、隣接する頂点に塗られた色と別の色を\(  x \)に塗ることで\(  G \)の\(  5- \)彩色が完了する。そこで\(  x \)の次数は5であるとしよう。

\(  x \)に隣接する頂点を時計回りに\(  y_1, y_2, y_3, y_4, y_5 \)とする。これらの5頂点に塗られている色が4色以下であれば、使われていない色を\(  x \)に塗ることで\(  G \)の\(  5- \)彩色が完了する。そこで、\(  y_1, y_2, y_3, y_4, y_5 \)にすべて異なる色1,2,3,4,5が塗られているとしよう。

ここで、記述を簡略化させるために「(1,3)ケンペ鎖」という考えを導入する。(1,3)ケンペ鎖とは、\(  G \)の頂点で、色1と3が塗られているものと、それらの間を結ぶ辺だけを集めてできるグラフのことである。ここからは\(  y_1 \)からでている(1,3)ケンペ鎖が、\(  y_3 \)を含むかどうかで場合分けを行う。

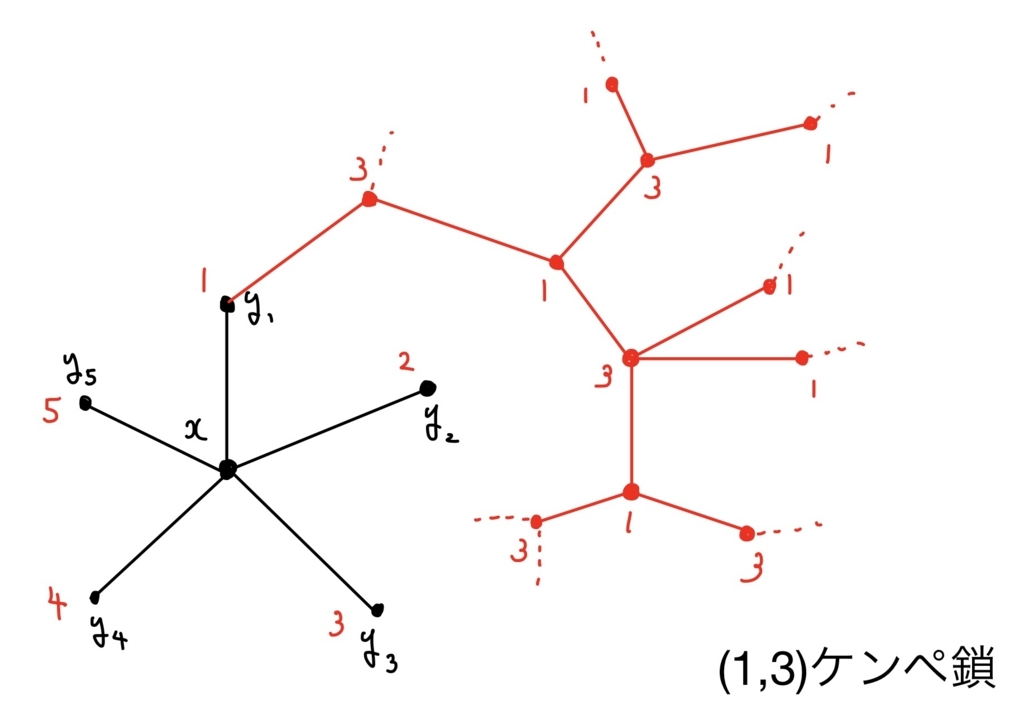
(ケース1) 頂点\(  y_1 \)から出ている(1,3)ケンペ鎖が\(  y_3 \)を含まない場合

そのケンペ鎖の頂点について、色1のものは色3に、色3のものは色1に塗り替えても、グラフ\(  G-x \)は\(  5- \)彩色となっている(塗り分けが維持できている)。そして\(  y_1 \)は色3になっているので、\(  x \)に色1を塗ることができ、グラフ\(  G \)の\(  5- \)彩色が完成する。

(ケース2)頂点\(  y_1 \)から出ている(1,3)ケンペ鎖が\(  y_3 \)を含む場合

このとき、\(  y_2 \)が(1,3)ケンペ鎖で囲まれた状態になっている(下図の赤部分)。

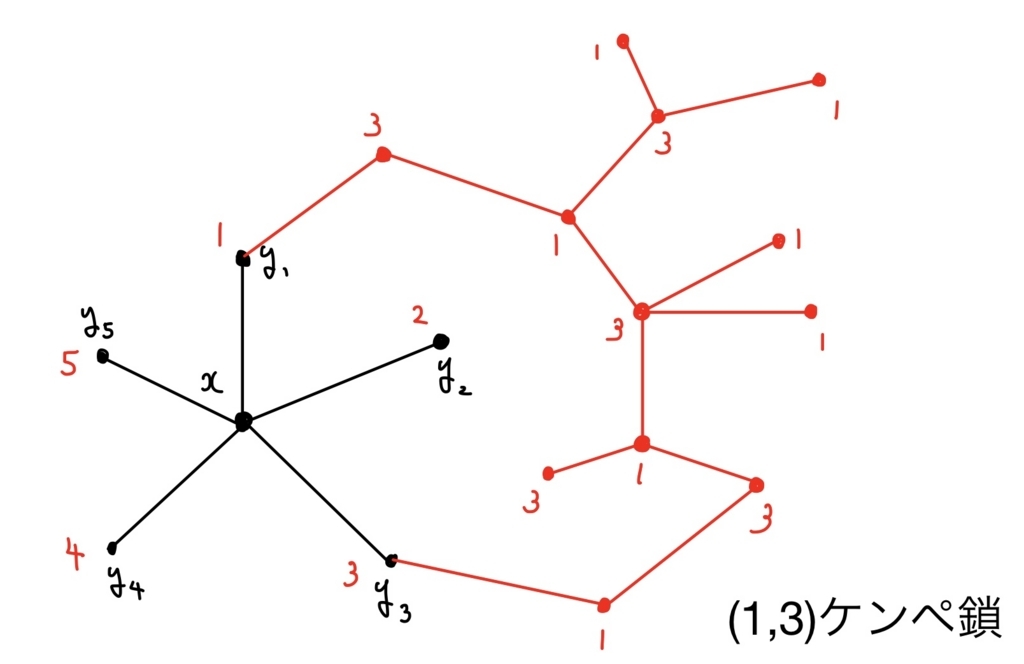
ここで\(  y_2 \)から出ている(2,4)ケンペ鎖を考えると、(1,3)ケンペ鎖が壁になっているせいで\(  y_4 \)には到達できない。よってこの(2,4)ケンペ鎖の頂点で色2のものは色4に、色4のものは色2に塗り替えても、グラフ\(  G-x \)は\(   5-\)彩色となっている。塗り替えた後は\(  y_2 \)は色4になっているので、\(  x \)に色2を塗ることができ、グラフ\(  G \)の\(  5- \)彩色が完成する。(証明終)

毎度ですが、グラフ理論は難しい予備知識があまり必要なく、理詰めで考えていけるのが面白いですね。頭の体操にもなります。

では、今回はこの辺で。

(参考)

前原 濶『直観トポロジー』

★★★

今回の内容の動画版