今回はCTスキャンという、お腹の輪切り画像を計算する数学の話です。CTスキャン自体はそこそこ難しい数学の内容ではありますが、今回はその導出などではなく、知られている数式を眺めて話題を知るのを目的とします。
CTスキャンは、病院等にある次のような雰囲気の機械です(画力があまりないので伝わるか自信がないのですが)。
丸っこい穴が特徴的ですね。この機械に体を通すと、体を”輪切りにした”画像を得ることができます。もちろん実際に輪切りにしているわけではなく(死んでしまう!)、次のようなアイディアで”輪切り画像”を計算しています。
CTスキャンでは微弱のX線を利用します。X線は様々な物体を通り抜ける性質がありますが、物質によって通り抜けやすさが異なります。そこで実際にX線を体内を通過するように放出し、その体内通過後のデータを計測します。これにより体内の何らかの情報がわかるのでは?、というわけです。
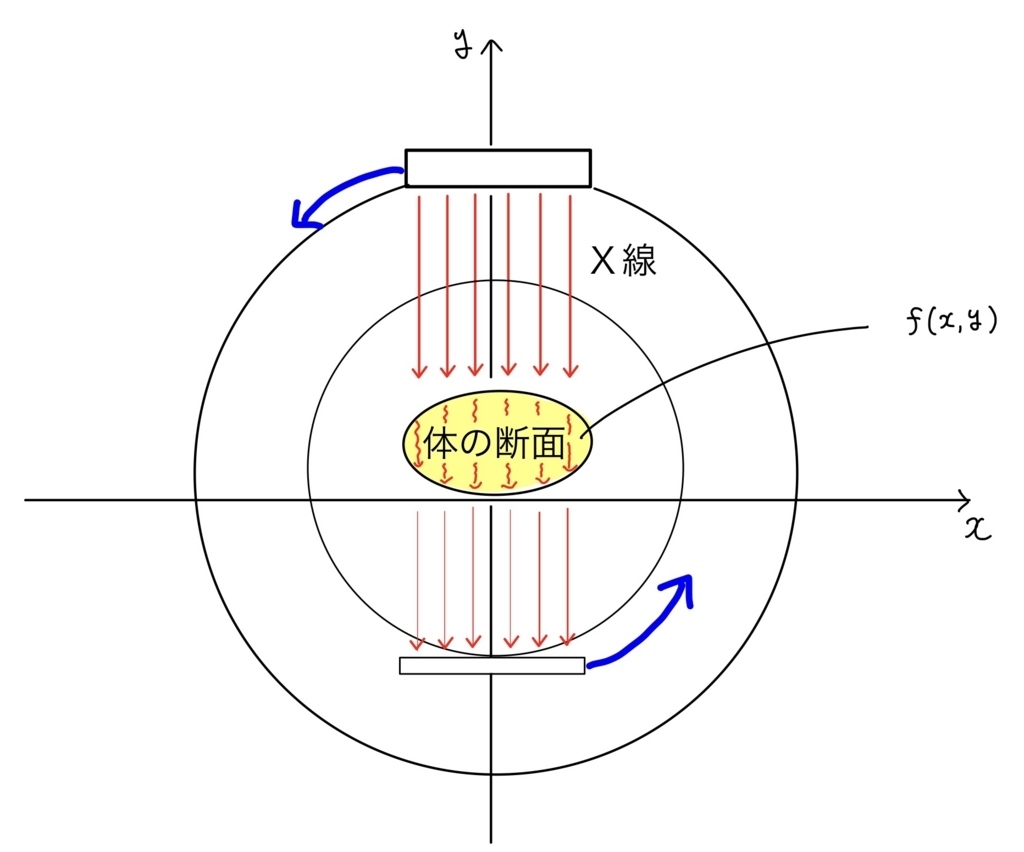
しかしもちろん、一方の方向からX線を当てるだけだと、深さの情報が失われます。X線を通しにくい何か異質な物体があったとしても、それがお腹側にあるのか、背中側にあるのかについては分からないのです。そこで、より詳しい情報を得るために
「X線の体内通過後の計測を、グルグル回りながらいろんな角度でやったらいいんじゃね?」
となるのは自然な発想ですよね。実は、このアイディアで体の断面図が”完全に”求められるのです。
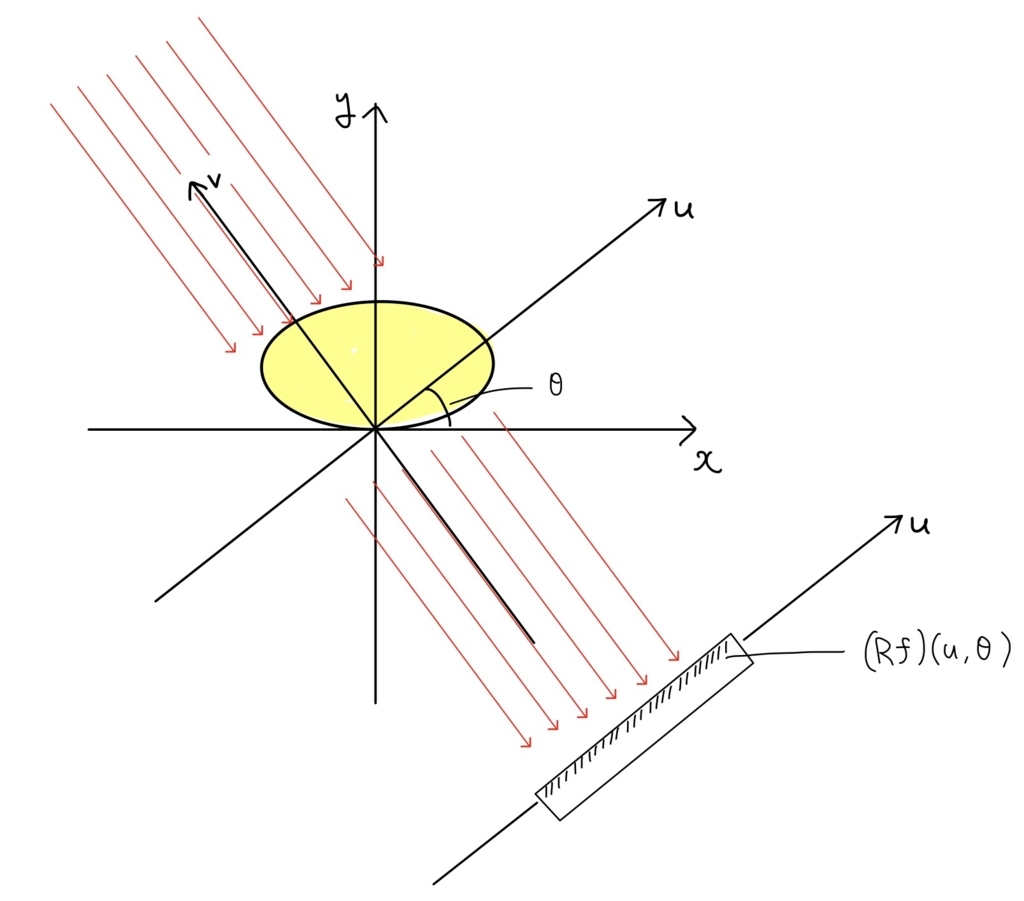
上図にあるように\( \displaystyle (Rf)(u,\theta) \)は角度\( \theta \)のときのX線体内通過後の1次元データです(これは観測で求められる!)。これを各角度で計測し、次のような計算によって体の断面図の2次元データ\( f(x,y) \)が計算できます。
[box class=”blue_box” title=”CTスキャンの原理”]お腹の輪切り画像\( f(x,y) \)は、観測値\( (Rf)(u,\theta) \)から次のように計算できる(横スクロールします)。
\( \displaystyle {\small f(x,y)=(2\pi)^{-\frac32}\!\int_{0}^{2\pi}\!\int_{0}^{\infty}\! \mathcal{F}_u(Rf)(r,\theta)e^{ir(x\cos\theta+y\sin\theta)}r dr d\theta} \)
ここで右辺の\( \displaystyle \mathcal{F}_u (r, \theta ) \)は関数\( \displaystyle (Rf)(u,\theta) \)を変数\( u \)についてフーリエ変換した
\( \displaystyle \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}(Rf)(u,\theta)e^{-iru}du \)
を表す。
[/box]
観測値\( (Rf)(u,\theta) \)から元の画像\( f(x,y) \)が復元できるので、輪切り画像を見たいときに、本当に人体を輪切りにする必要がないのです。ありがとうCTスキャン!ありがとう三角関数!(無理やりまとめた)
では今回はこの辺で。
(参考)
杉山健一『フーリエ解析講義』
★★★
今回の内容を話した動画です(前半は別の話をしています)
