今回の内容の動画版→留数定理を利用して実関数の積分を計算する
前回までの記事
・複素積分の定義、コーシーの積分定理 複素解析を使ってみる(1回目/全3回)
・ローラン展開、留数定理 複素解析を使ってみる(2回目/全3回)
実関数の積分を複素数を利用して計算する
複素数を導入するメリットの一つとして、難しい計算を統一的な手法で実行できることが挙げられます。今回は実数の範囲の積分を複素解析の力で計算してみます。あんまり一般的な書き方をしても頭に残りにくいので、次の積分
\(\ \ \displaystyle \int_{\infty}^{\infty}\frac{1}{1+x^2}dx \)
を求めることを目標にしましょう。
なお、この積分は原始関数がアークタンジェント(arctan)であるということを使えば
\( \displaystyle \small \int_{-\infty}^{\infty}\frac{1}{1+x^2}dx=\left[\arctan x \right]_{\infty}^{\infty}=\frac{\pi}{2}-\left(-\frac{\pi}{2}\right)=\pi \)
ということで計算が完了します。また、その知識がなくても高校数学のお作法にしたがって\( x=\tan\theta \)とおくと\( \frac{dx}{d\theta}=\frac{1}{\cos^2\theta} \),変数の対応が\( x:-\infty\to\infty \)が\( \theta : -\frac{\pi}{2}\to \frac{\pi}{2} \)となっていることから
\( \displaystyle \int_{-\infty}^{\infty}\frac{1}{1+x^2}dx \)
\( \hspace{10mm}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{1+\tan^2\theta}\cdot \frac{1}{\cos^2\theta}d\theta \)
\( \hspace{10mm}=\left[\theta\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}=\pi \)
とも求められます。
今回はこの結果を、前回までの記事で扱った複素解析の諸道具を使って確認してみようということです。
[box class=”blue_box” title=”問題”]\( \displaystyle \int_{-\infty}^{\infty}\frac{1}{1+x^2}dx=\pi \)
を示せ。
[/box]
[box class=”glay_box” ]
(解)
複素関数\( f(z)=\frac{1}{1+z^2} \)は\( z=i,-i \)で1位の極をもち、それ以外では正則である。次のように積分路を設定する。
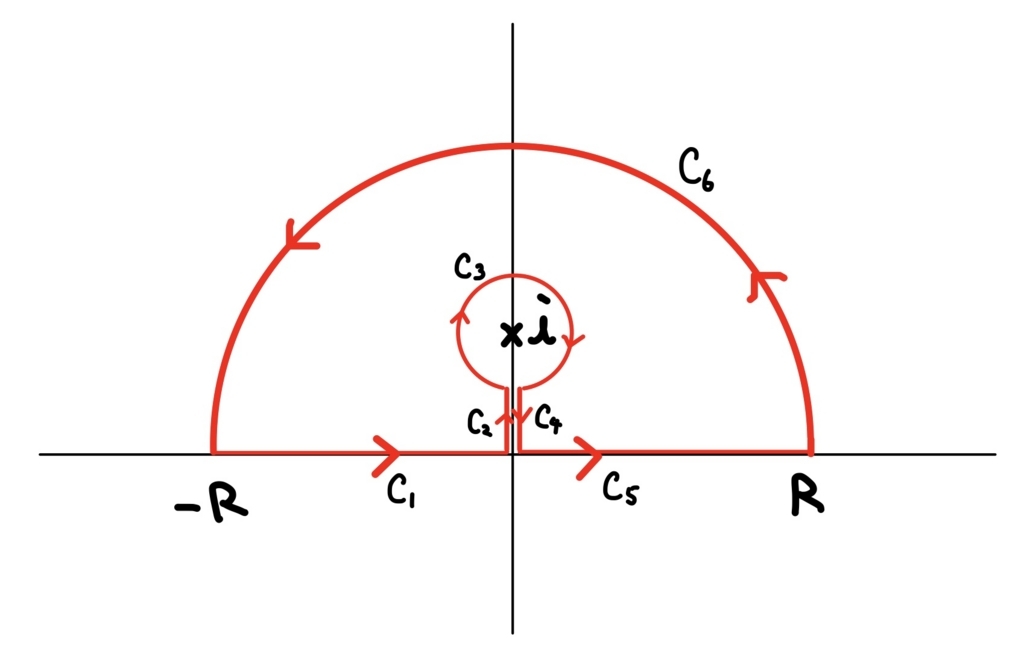
なお、図ではすこし離して書いてあるが、\( C_2 \)と\( C_4 \)は虚軸上を走っているものとし、\( C_3 \)の半径は1より小さい(例えば\( \frac12\))とする。
領域の内部で\( f(z) \)は正則なので、コーシーの積分定理により
\( \displaystyle \int_{C_1+C_2+\cdots +C_6 }f(z)dz=0 \)……③
が成り立つ。目標の積分は\( \displaystyle \lim_{R\to\infty}\int_{C_1+C_5}f(z)dz \)であることに注意しよう。
③を変形すると
\( \displaystyle \displaystyle \int_{C_1+C_5 }f(z)dz=\int_{-C_3}f(z)dz-\int_{C_6}f(z)dz \)…④
となる(\( C_2 \)と\( C_4 \)は同じ経路をそれぞれ逆に走る線積分であるから打ち消しあって消えることに注意)。ただし\( -C_3 \)は\( C_3 \)を逆に移動するもの(すなわち正の向きに回転する経路)を表すものとする。
④の右辺第一項については\( f(z) \)が\( z=i \)で1位の極であることから簡単に留数が計算できて(すでに前回記事でも行なった計算だが、もう一度かく)
\( \displaystyle \int_{-C_3}f(z)dz=2\pi i Res(f,i) \)
\( \displaystyle =2\pi i \lim_{z\to i}(z-i)\frac{1}{z^2+1}=\lim_{z\to i}\frac{2\pi i}{z+i}=\pi \)…⑤
となる。
また、④の右辺第二項については\( R\to0 \)のとき\( \to 0 \)となる。実際、経路を\( C_6 : z=Re^{it} (0\leq t \leq \pi) \)とおいて、
\( \displaystyle \left|\int_{C_6}f(z)dz\right|=\left|\int_{0}^{\pi}\frac{1}{1+R^2e^{2ti}}\cdot Rie^{ti}dt\right| \)
\( \displaystyle\ \ \leq\frac{\pi R}{R^2-1}\to 0 \ (R\to \infty) \)……⑥
ここで、\( |Rie^{it}|=R \)、\( |1+R^2e^{2ti}|= |R^2e^{2ti}-(-1)|\geq R^2-1 \)などと評価している。
よって、④〜⑥により、
\( \displaystyle \lim_{R\to\infty}\int_{C_1+C_5}f(z)dz=\pi \)
が成り立つ。この左辺は\( \displaystyle \int_{-\infty}^{\infty}\frac{1}{1+x^2}dx \)を表すからこれで目標の式が示された。(終)
[/box]★★★
今回の内容の動画版です。