次は、私がかなり気に入っている問題の一つです。
次の分数を約分せよ。
シンプルな上に、なんといっても予備知識がほぼいらない点が良いです。ほとんどの方にとって分数の約分というのがなんであるかは説明の必要がなく、問題文の意味はすぐ共有できるのです。しかし、実際に約分をしようとすると簡単にはいかない。思いつく素数で割ってみても割れない。相当な大きさの素数で割らないと無理そうだ…ということでかなり困難を強いられます。数学Aの整数の分野を扱う際の導入として扱うと面白そうです。
さて、今回の問題は、大きな2数の最大公約数をアルゴリズム的に求めることのできる、ユークリッドの互除法が活躍します。
ユーグリッドの互除法で最大公約数を求めるには、次のような計算をするとよいです。次の図は計算が終わったところの様子です。
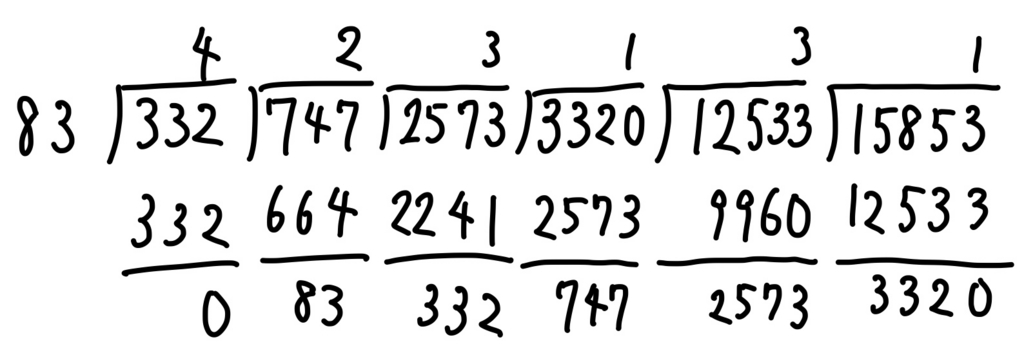
計算は右から左へ進んでいます。まず最初に15853を12533で割って、その余りを今度は割る数として12533の右に持っていきます。あとはこれを繰り返すのです。余りは0以上でステップを重ねるごとにどんどん小さくなりますから、いつかは0になります。
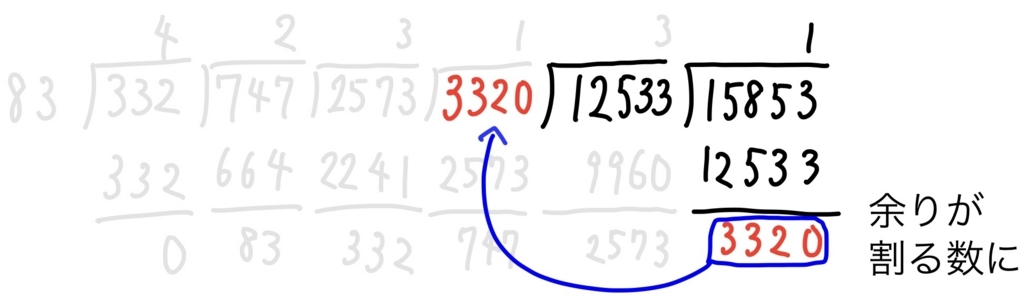
余りが0になったとき一番左にある数 83 が15853と12533の最大公約数(G.C.DやG.C.M.とも)となっています。
上の手順でなぜ15853と12533の最大公約数が求められるのでしょうか。タイルの敷き詰めなど図的な説明もありますが、次の集合の考えを使う説明もあります(初等整数論の教科書ではこちらが普通)。
15853と12533の割り算の結果は
15853=12533×1+3320 ……①
と表されます。ここで、集合
を考えると、が成り立ちます。実際、任意の
を持ってくると、
15853=, 12533=
となる自然数が存在しますが、式の形①より
3320=×1=
となります。すなわちは3320も割ることになり、
が12533と3320の公約数となり
、よって
です。また逆に任意の
に対してやはり式の形①より
は15853も割るため、
は15853と12533の公約数となり
、すなわち
です。
なので、特にそれぞれの集合に属する最大値も一致しますから、
「(15853と12533の最大公約数)は(12533と3320の最大公約数)と等しい」
のです。以下議論を繰り返すと以下のことがわかります。
「(12533と3320の最大公約数)は(3320と2573の最大公約数)と等しい」
「(3320と2573の最大公約数)は(2573と747の最大公約数)と等しい」
「(2573と747の最大公約数)は(3320と2573の最大公約数)と等しい」
「(747と332の最大公約数)は(332と83の最大公約数)と等しい」
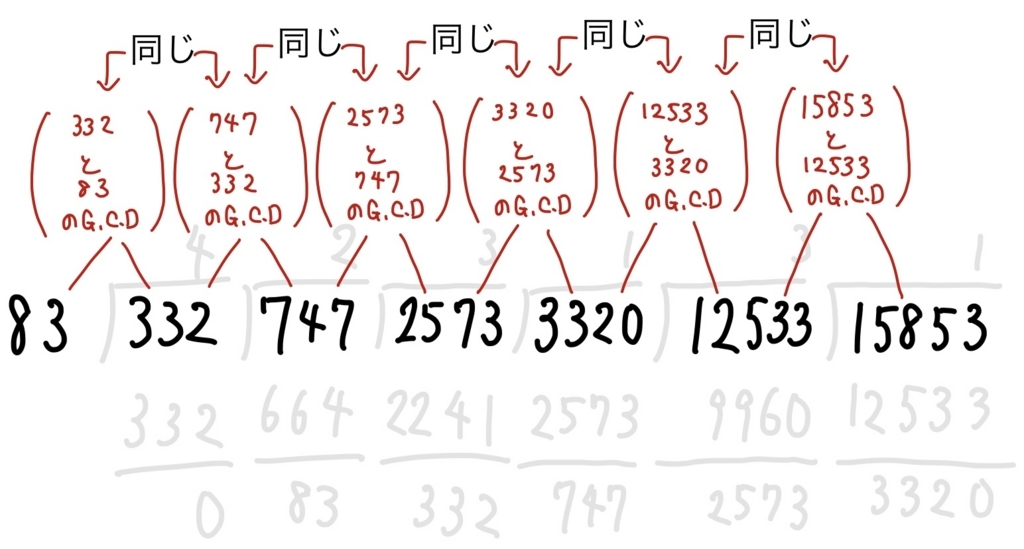
結局、
「(15853と12533の最大公約数)は(332と83の最大公約数)と等しい」
ことがわかります。ここで余りが0となった332と83の関係は
332=83×4
となっていますから、332と83の最大公約数が83であることがわかります。
以上のことから「(15853と12533の最大公約数)が83であること」がいえるのです。
約分問題を作る方法
上の例は最大公約数が83となることから
と計算されます。
逆に約分が大変な問題を作るためにはそこそこの大きさの相異なる素数を用意して
とすれば良いことがわかります。
素数を求める際には以下のページが参考になるかもしれません。(挙動をスムーズにさせるため、本ページに貼り付けていたものを次ページへ分けました。2018.8.31)
4桁以下の素数一覧(1229個) – すうがくブログ | 授業準備
