放物線ヨコ平行移動が式と逆な感じがする話題をサマータイムと絡めて話してみた

今回の内容の動画版→放物線ヨコ平行移動が式と逆な感じがする話題をサマータイムと絡めて話してみた

数学1の割と最初の方で扱う、放物線の平行移動についての話です。とりあえず下図の左下の"スライダー"を左右に動かしてみてください。

最初の状態は\( y=(x+0)^2 \)ということで要するに\( y=x^2 \)のグラフです。

これをいろいろいじってみると次のようなことがわかります。

\( y=(x+1)^2 \)のときは\( y=x^2 \)のグラフが左に1つ動く。

\( y=(x+2)^2 \)のときは\( y=x^2 \)のグラフが左に2つ動く。

…

\( y=(x-1)^2 \)のときは\( y=x^2 \)のグラフが右に1つ動く。

\( y=(x-2)^2 \)のときは\( y=x^2 \)のグラフが右に2つ動く。

…

\( x \)の部分が\( x+1 \)とか\( x+2 \)のように変化すると左側の方向、すなわち\( x \)軸のマイナスの向きに移動します。

逆に、

\( x \)の部分が\( x-1 \)とか\( x-2 \)のように変化すると右側の方向、すなわち\( x \)軸のプラスの向きに移動します。

式の見た目と動きが逆になってしまってますね。これをきちんと示すには軌跡という数学2の分野の道具を使うことになるのですが、数学1で初めてこの内容を勉強する人にとっては、その説明をみてもおそらく「よくわかった！」とはならないこともあると思います。今回は納得してもらう説明の仕方の一つで、「サマータイム」を利用してはどうか、という話です。

すなわち、

「\( x \)が\( x+1 \)に変わるのは、時間が1時間早くすすむことに対応する」

と考えてみるわけです。サマータイムで1時間時間が早まると、

・5時だけど、1時間早めて6時だと思って行動する。

・6時だけど、1時間早めて7時だと思って行動する。

・7時だけど、1時間早めて8時だと思って行動する。

…

という要領で、1時間先の行動をすることになります。

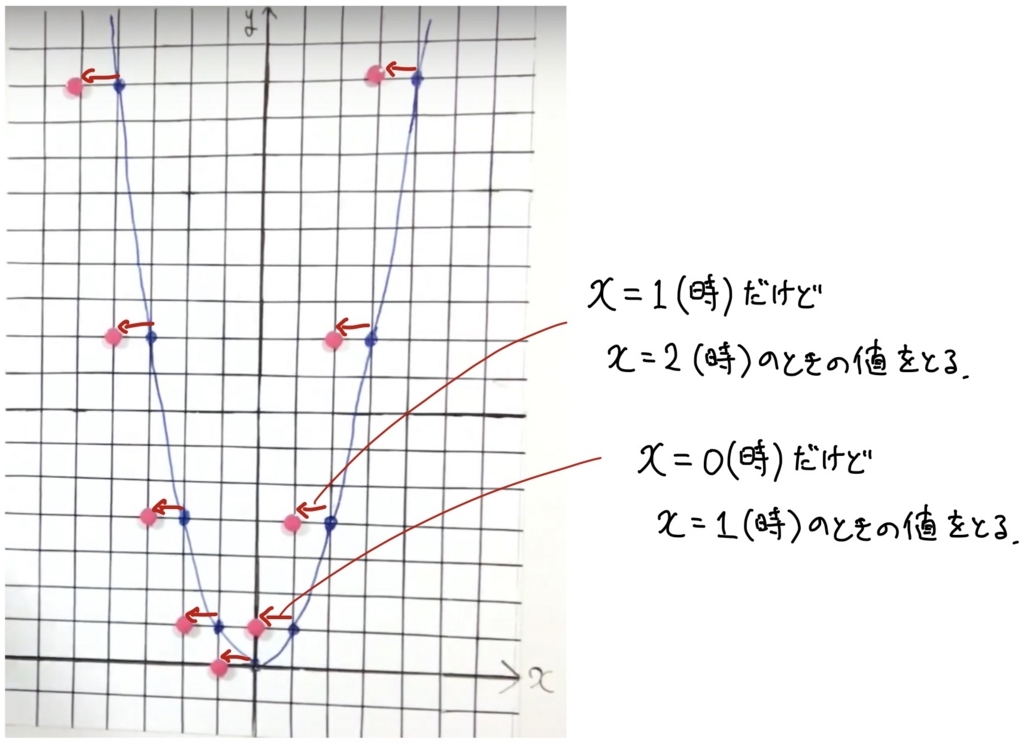
関数の話に戻ると、\( x \)のところが\( x+1 \)に変わると、

・\( x=0 \)(時)のとき、いままでだと\( x=1 \)(時)のときにとっていた値をとる。

・\( x=1 \)(時)のとき、いままでだと\( x=2 \)(時)のときにとっていた値をとる。

・\( x=2 \)(時)のとき、いままでだと\( x=3 \)(時)のときにとっていた値をとる。