数学Aで「オイラーの多面体定理」というものがありますが、それの理論のもととなっている平面グラフのオイラーの定理を紹介します。この証明が完了すれば、ちょっとの準備をするだけでオイラーの多面体定理を導くことができます。
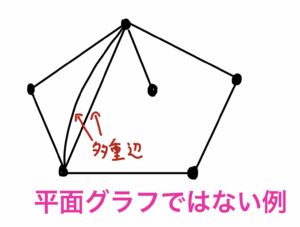
平面グラフとは「頂点」と「辺(頂点を結んだもの)」からなるグラフで、どの辺も交差せず、多重辺も存在しないものです。
以下の図のように、特定の2頂点が2本以上の辺でつながっているような場合は多重辺が存在することになり、平面グラフではありません。
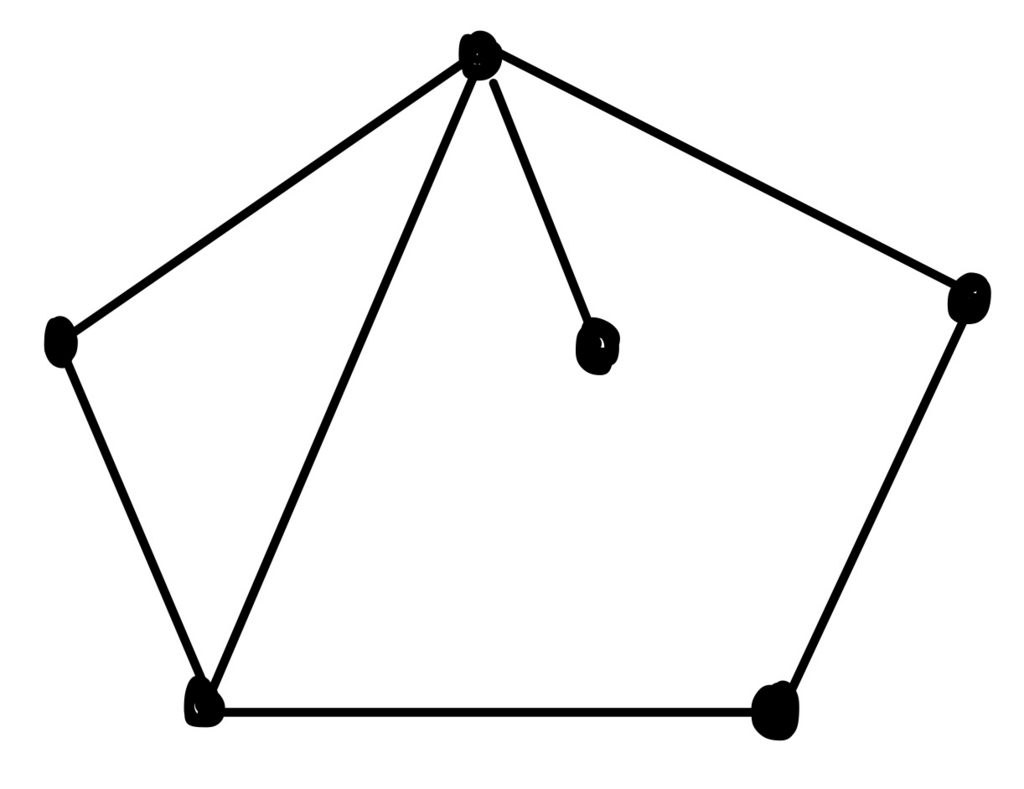
多重辺を解消した以下のグラフは平面グラフとなります。
また、グラフによっては、辺が交差していても、辺を多少ずらせば平面グラフになる場合もあります。
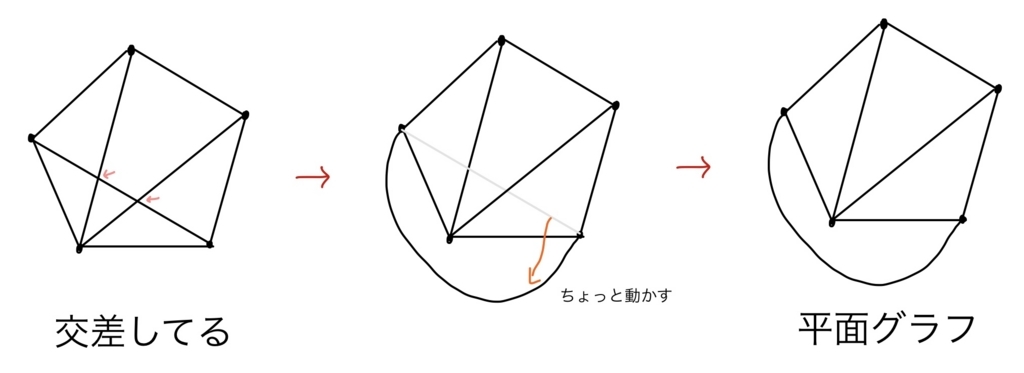
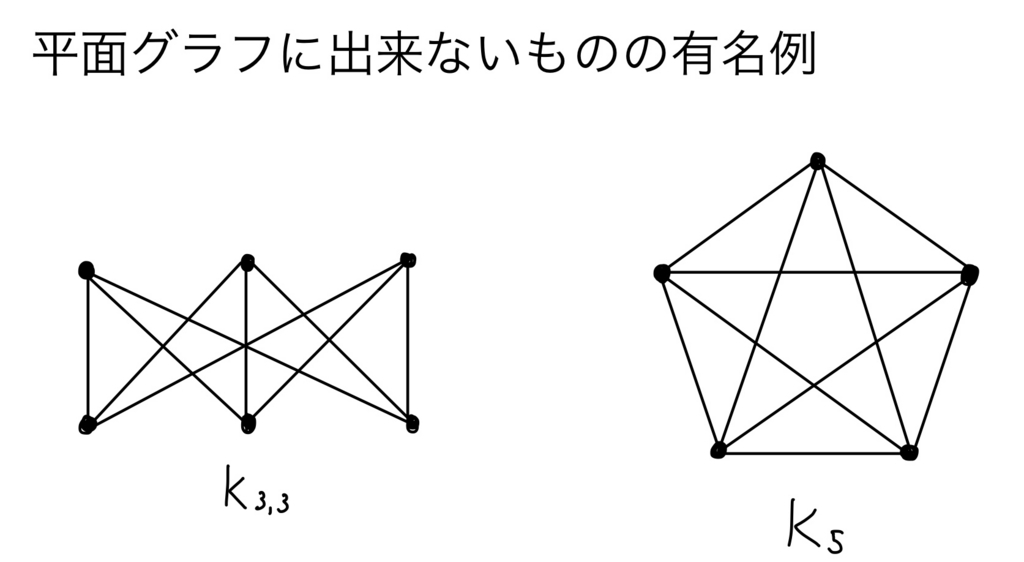
なお、辺の移動をどんなに工夫して頑張っても辺が交差している状態を解消できない場合もあります。以下の2例は有名なもの。今回はこういったパターンは考えないことにします。
平面グラフ、すなわち辺が交差しないグラフは平面をいくつかの(交わらない)領域に分けます。これらの領域を平面グラフの面といいます。

上の図でいうと五角形の左と右、そして五角形の外側の3箇所に平面が分けられています(五角形の外側に無限に広がる領域も面ということに注意しておいてください)。
では、今回の公式の話に移りましょう。
[box class=”blue_box” title=”平面グラフに関するオイラーの公式”]平面グラフの頂点数、辺数、面数をそれぞれ\( v,e,f \)とすると、次が成り立つ。\( \ \ \ \ v-e+f=2 \)
[/box](確認)
先ほどの例でいうと(再掲)

頂点数\( v=6 \)、辺数\( e=7 \)、面数\( f=3 \)ですから
\( \ \ \ v-e+f=6-7+3=2 \)
となり、公式が確かに成り立っています。
[box class=”glay_box” ](証明)
任意の平面グラフは、1点からなるグラフ(下図の①)から、「切り込み辺の追加」と「横断辺の追加」という操作を何回か行なって生成されたと考えることができる。
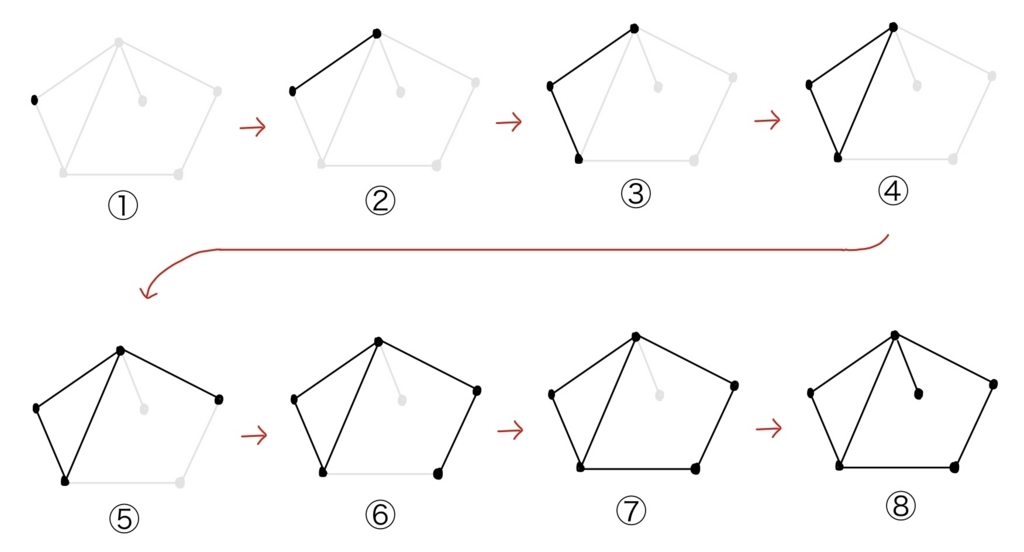
上の図でいうと例えば①→②が「切り込み辺の追加」、③→④が「横断辺の追加」である。一応きちんと操作の意味をいっておくと、「切り込み辺の追加」というのは平面グラフのある頂点から出発する辺を、すでに描かれた辺と交差することがないように描き、その終点は新しい頂点とするということであり、「横断辺の追加」というのは隣接していないある頂点のペアをすでに描かれた辺と交差することがないように辺で結ぶことである。
ここで、これら2操作によって、\( v-e+f \)の値が変化しないことに注意しよう。「切り込み辺の追加」は辺が1本増えると同時に終点が頂点として追加されるので、\( e,v \)が1つずつ増える。よって\( v-e+f \)の値に変化はない。また「横断辺の追加」については辺が1本増えると同時に新しい面が1つでき、\( e,f \)が1つずつ増えるため、やはりこの操作でも\( v-e+f \)の値に変化はない。
さて、冒頭でも述べたように、任意の平面グラフは1点からなるグラフから上述の(\( v-e+f \)の値が変わらない)2操作を繰り返して得ることができるのであった。1点からなるグラフの場合は\( v=1,e=0,f=1 \)で\( v-e+f=2 \)となっているので、任意の平面グラフで\( v-e+f=2 \)が成り立つことになる。(証明終)
[/box]上の公式は立体へほぼそのまま適用できます。どこか「面の1箇所に穴を開けてそこをぐっと広げて平面に潰して」から、平面のオイラーの公式を使えばいいんです
「面の1箇所に穴を開けてそこをぐっと広げて平面に潰して」というのは、次のような意味です。たとえば立方体で考えましょう。いま、立体はゴムのような伸び縮みが可能な特殊な素材でできているとします。これの一箇所の面に穴をあけて連続的に潰していくというのは次のような変形です。
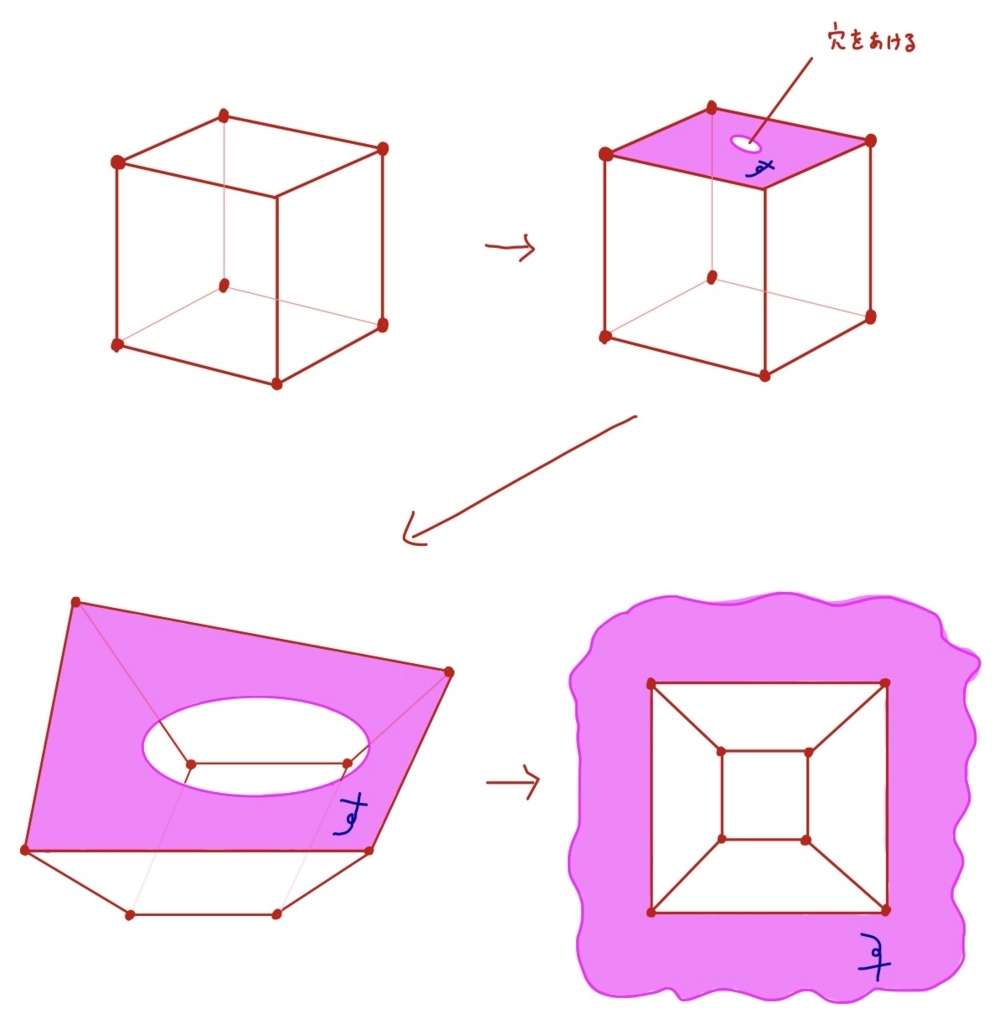
このように平面に潰した状態で、平面グラフで証明したオイラーの定理を適用するのです(この変形の過程で頂点数\( v \),辺数\( e \),面数\( f \)に変化がないことに注意)。上図の紫で塗られたぴろぴろの面を、外側に無限に広がる面と同一視すれば、潰す前の元の立体でも\( v-e+f=2 \)が成立することがわかります。
(同一視というのがわかりにくい方は、以下のように考えるとよいかもしれません。平面につぶした状態で紫のぴろぴろの面をいったんとっぱらい、その代わりに外側に無限に広がる面をつけたと考えます。この過程で面数に変化はない(もちろん頂点や辺数にも変化はない)ので、\( v-e+f=2 \)の値に変化はありません。そうすると平面グラフの証明のときと全く同じ状況になるので\( v-e+f=2 \)が成立、これより元の潰す前の立体においても\( v-e+f=2 \)となることがわかります。)
上記のような、「面の一箇所に穴を開けてぐっと広げて平面に潰す」操作が文句なしにできるようにするために、凸多面体(多面体内部の任意の2点を結ぶ線分が多面体内部にある立体。要するに凹みや穴が無い立体と考えてもらえばOK)という条件で考えることが多いようです。
\(\ \ v-e+f=2 \)
[/box]離散数学は予備知識があまりいらないのでいいですね〜。
(参考)
前原 濶『直観トポロジー』
★★★
今回の内容の動画版です↓