ひもをぶらんと垂らしたときの曲線(上図の赤の曲線)を式で求めてみましょう。大学数学の知識が必要ですが、ぜひ雰囲気をお楽しみください。
ひもを垂らしたときにできる曲線は、関数
\(\ \ \displaystyle \ f(x)=\frac{e^{ax}+e^{-ax}}{2a}\)…(☆)
のグラフである。ただし、対称軸を\( y \)軸にとり、ひもの”底”が原点に対応するようにする。また、\( a \)はひもの密度などで定まる定数である。[/box]
(証明)求める関数を\( y=f(x) \)とし、微分方程式を立てよう。区間\( [x,x+\Delta]\)に対応するひもの一部分を考える。左端の点\( A \)の座標は\( (x,f(x))\),右端の点\( B \)の座標は\( (x+\Delta, f(x+\Delta)) \)となる。
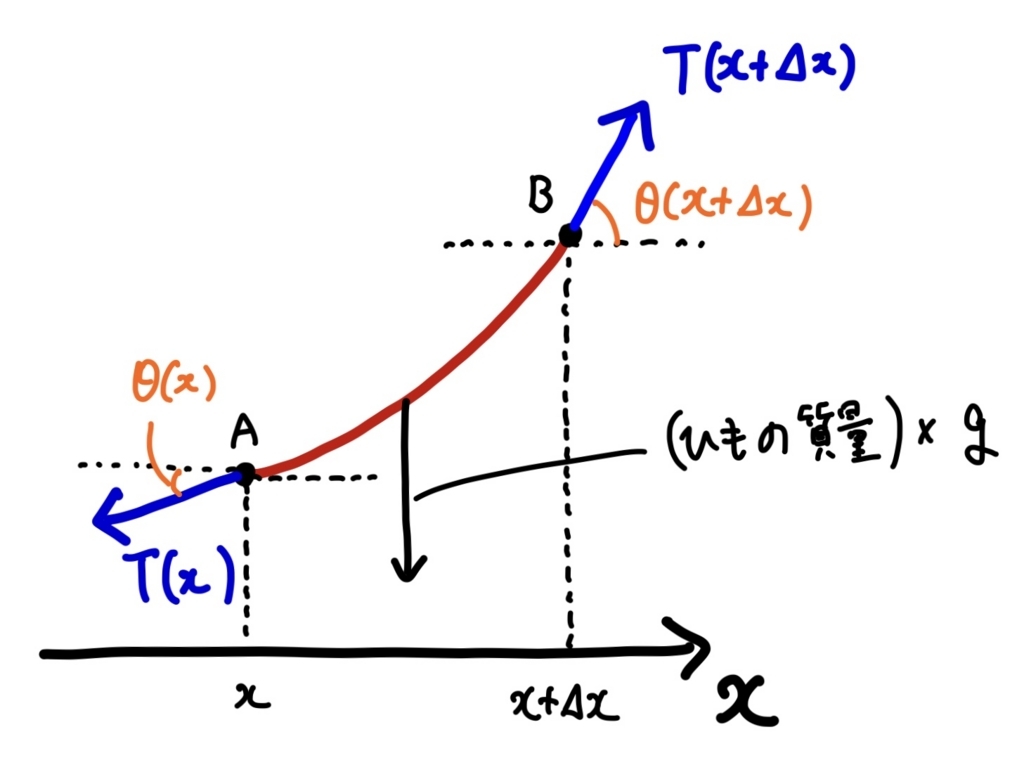
点\( A,B \)にはそれぞれ張力\( T \)が働いている。張力\( T \)は位置\( x \)ごとに定まるひもを引っ張る力である。また、この力の方向と水平方向とのなす角を\( \theta(x) \)で表す。
ここで、上のひもは静止しているのだから、つり合いの式を作ることができる。まず横方向については\( A \)を左に引っ張る力と\( B \)を右に引っ張る力がつり合っているので、
\(\ \ T(x+\Delta x)\cos\theta(x+\Delta x)=T(x)\cos\theta(x) \)…①
となる。一方、縦方向については\( B \)を上に引っ張る力と、「\( A \)を下に引っ張る力と、ひもが重力で引っ張られる力をあわせた力」がつり合っているので、
\( \ \ T(x+\Delta x)\sin\theta(x+\Delta)\)
\(\ \ =T(x)\sin\theta (x)+\rho g \sqrt{(\Delta x)^2+\left(f'(x)\Delta x\right)^2} \)…②
となる。ここで\( \rho \)はひもの密度、\( g \)は重力加速度であり、\( A,B \)間のひもの長さは線分\( AB \)の長さで近似している。
まず①の式から、関数\( T(x)\cos \theta(x) \)は\( x \)によらない定数であることがわかる。よって
\( \ \ T(x)\cos\theta(x)=\tau \)(定数)…③
とおくことができる。
②については右辺第一項を左に移項して両辺を\( \Delta x \)で割れば関数\( T(x)\sin\theta(x) \)の平均変化率なので\( \Delta x\to 0 \)として
\(\ \ \displaystyle \frac{d}{dx}\left[T(x)\sin\theta(x)\right]=\rho g \sqrt{1+(f'(x))^2} \)…④
を得る。
ここで\( \tan\theta(x)=f'(x) \)と③より、④の左辺に登場する\( T(x)\sin\theta(x)\)については
\( \ \ T(x)\sin\theta(x)=T(x)\tan\theta(x)\cos\theta(x)\)
\(\ \ =\tau\tan\theta(x)=\tau f'(x)\)…⑤
となる。④へ⑤の結果を適用すると
\( \ \ f”(x)=\frac{\rho r}{\tau}\sqrt{1+(f'(x))^2} \)
が導かれる。あとはこの微分方程式を解けばよい。簡単のため、定数部分\( \frac{\rho g}{\tau}=a \)とおき、\( f’=u \)とおくと\( u \)についての一階の微分方程式
\(\ \ u’=a\sqrt{u^2+1} \)
を得る。これは変数分離形であり、両辺を\( \sqrt{u^2+1} \)で割って\( x \)で積分することで
\(\ \ \displaystyle \int \frac{du}{\sqrt{u^2+1}}=ax+ \)定数 …⑥
という形になる。\( \left\{\log(u+\sqrt{u^2+1})\right\}’=\frac{1}{\sqrt{u^2+1}} \)であるので、
\( \ \ \log(u+\sqrt{u^2+1})=ax+b \)
を得る(\( b \)は定数)。対数の定義から\( u+\sqrt{u^2+1}=e^{ax+b} \)すなわち
\( \ \ u-e^{ax+b}=\sqrt{u^2+1} \)
となる。両辺を2乗して\( u \)について整理すると
\( \ \ f'(x)=u=\frac12(e^{ax+b}-e^{-ax-b}) \)
を得る。これを\( x \)で積分すれば
\( \ \ f(x)=\frac{1}{2a}(e^{ax+b}+e^{-ax-b}) \)
となる(“ひもの底”が原点に対応するようにしているので\( f'(0)=0 \)、すなわち積分定数は\( 0 \)としてよい)。\( f(0)=0 \)だから\( b=0 \)となり、(☆)が導かれた。(証明終)
[/box]この曲線はカテナリーとか、懸垂線とかいいます。また、関数
\(\ \ \displaystyle \cosh (x)=\frac{e^{x}+e^{-x}}{2} \)
はハイパボリックコサインといいます。上の結果はこの関数を使って\( y=\frac{\cosh (ax)}{a} \)と表すこともできますね。
ハイパボリックコサインという響きっていいですよね。「あのコサインが進化したのか…すごそうだ」ぐらいの印象がありますよね。
さぁ、その辺に落ちているひもを持ち上げてハイパボリックコサイン、カテナリーを作りましょう。
では。
(参考)
★★★
今回の内容を元にした動画です↓