-

-
ネイピア数eの導入と収束性
2019/4/30
今回は、微分積分の分野で重要なネイピア数\( e \)についての話です。
-
-
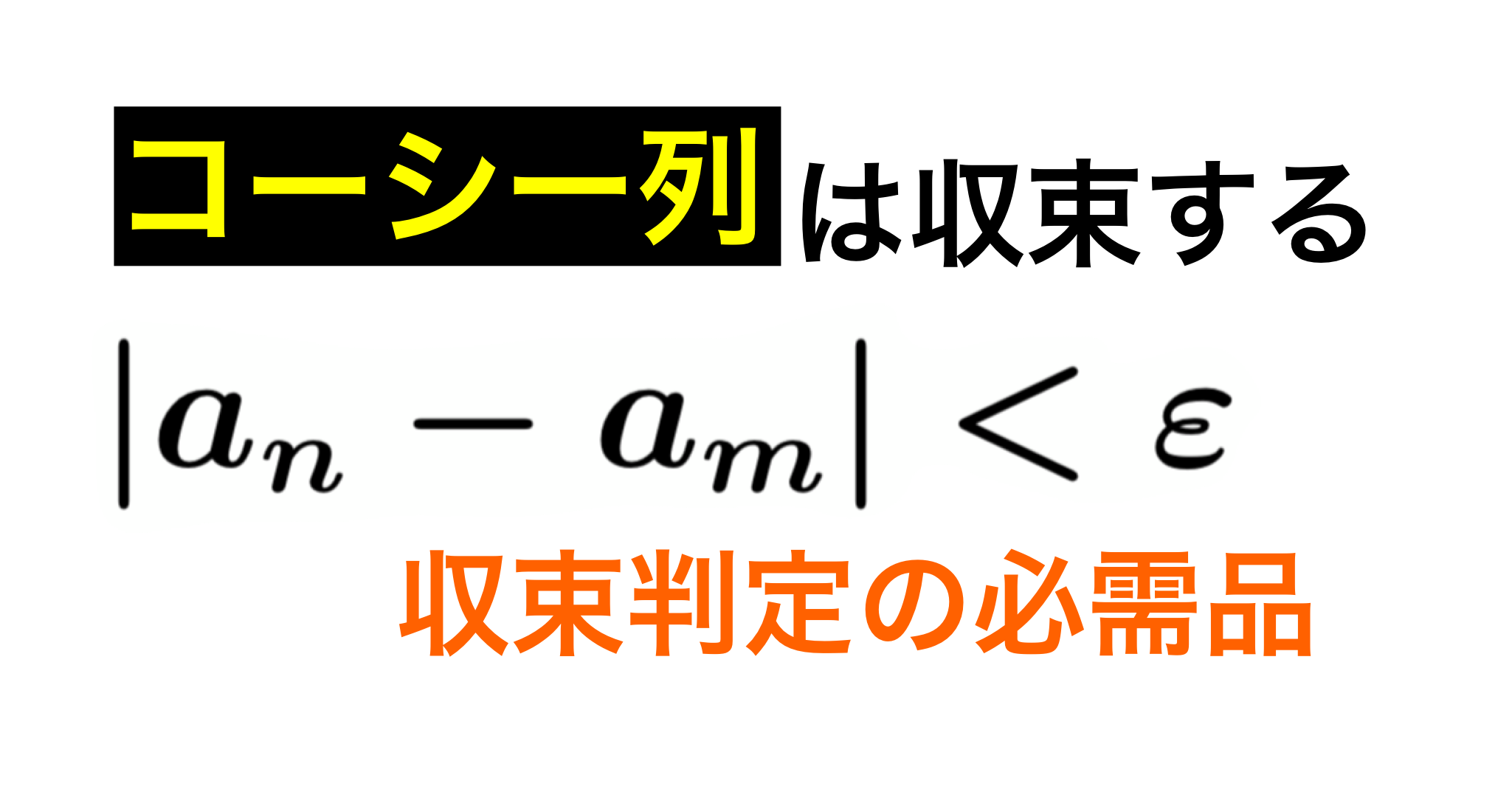
数列の収束条件の言い換え【コーシー列】
2019/4/30
コーシーの収束条件定理では極限値\( \alpha \)の姿を表に出すことなく、収束条件を与えています。
-
-
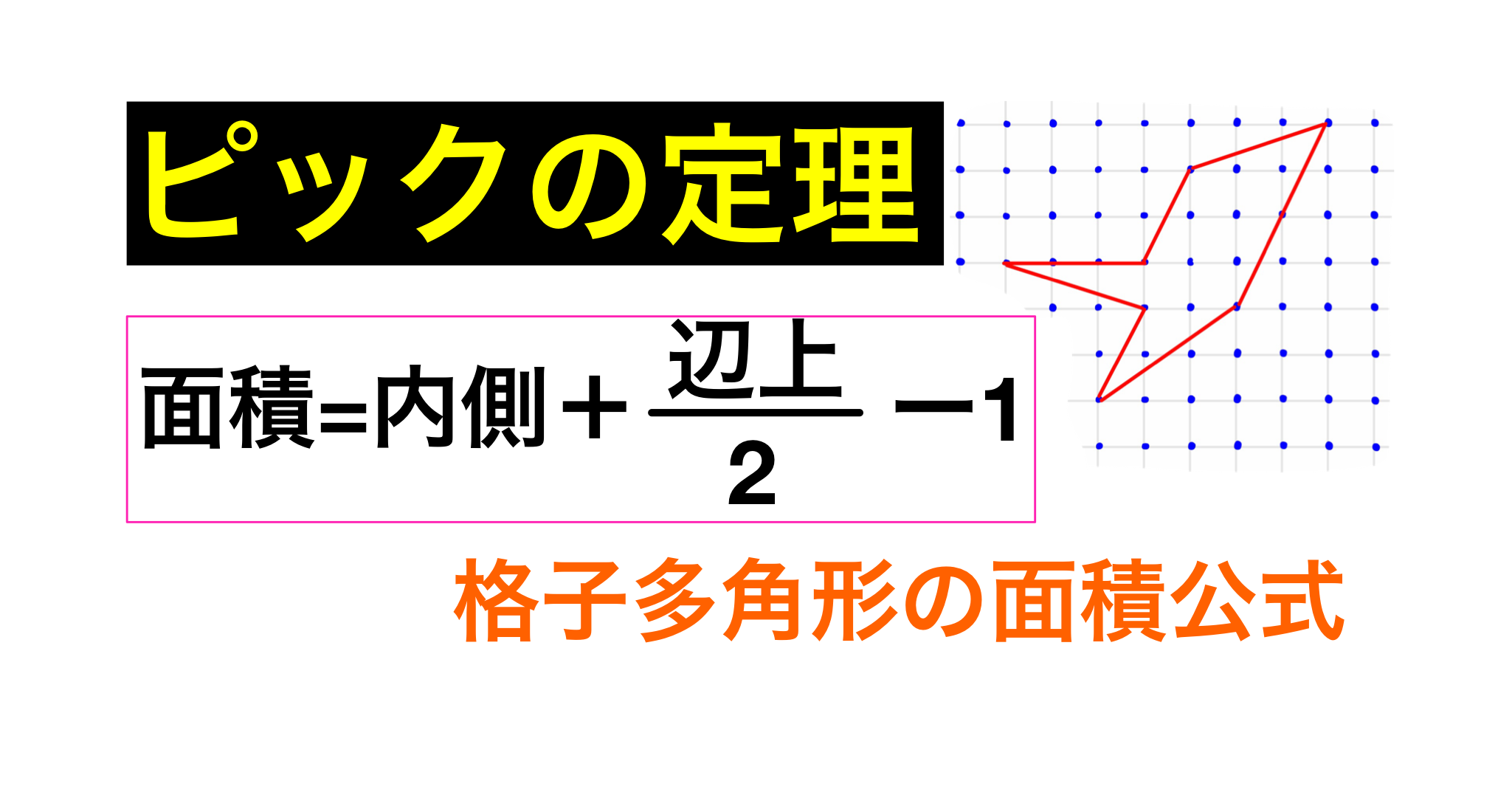
ピックの定理で、面積を簡単に計算!
2020/4/10
ピックの定理は、頂点が格子点上にある多角形(格子多角形)の面積を簡単に求めることができる公式です。
-

-
線型一階型の微分方程式、積分因子をかけて解く
2019/4/29
微分方程式いろいろ解けたらかっこいいじゃないですか、ということで今回は変数分離形よりもう少し工夫が必要な一階線型のパターンを扱います。変数分離形については以前の記事でも扱っているのでまだの方は是非そちらもご覧ください。
-

-
大きい数でも約分したい【ユークリッドの互除法】
2019/4/29
次は、私がかなり気に入っている問題の一つです。
シンプルな上に、なんといっても予備知識がほぼいらない点が良いです。