今回の内容の動画版です→ネイピア数eの登場シーンと収束性
今回は、微分積分の分野で重要なネイピア数\( e \)についての話です。
[box class=”blue_box” title=”ネイピア数\( e \)の定義”]\( \displaystyle e=\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n \)
[/box]
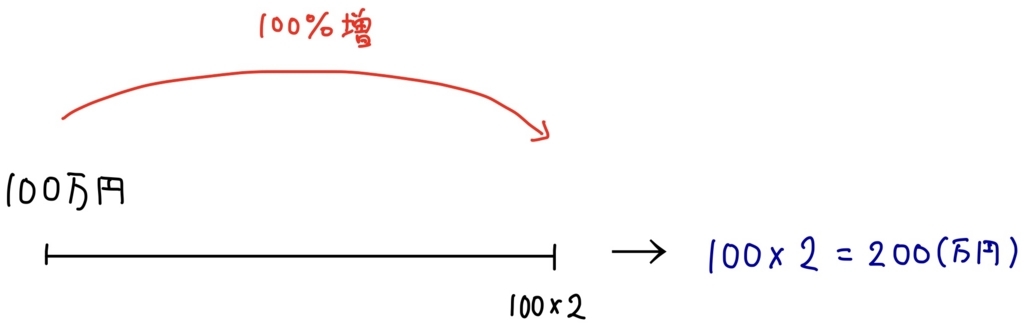
上の定義をいきなり覚えろ!と言われても、なかなかスッと頭に残りにくいですよね。そこで、例え話として、あなたが悪徳なサラ金業者の経営者であるとしましょう。1年間に100%の利息をつけてお金を貸していたとします(本当にやったら利息制限法違反!)。100万円を貸したとすると、1年後にあなたは100%の利息をつけて、100×2=200万円を得ることができるわけです。
ここで悪徳サラ金業者のあなたは、もっと儲けることを考え利息を半分にして、がかかるタイミングを2倍にする作戦を考えました。すなわち、利息を100%から50%にする代わりに、年に2回(半年に1回)利息がかかるようにします。そうすると、半年後には50%の利息をつけて100×1.5=150万円,そして1年後にはその150万円に対してさらに50%の利息をつけて150×1.5=225万円となります。さきほどの200万円よりも多くのお金を得ることができるわけですね!
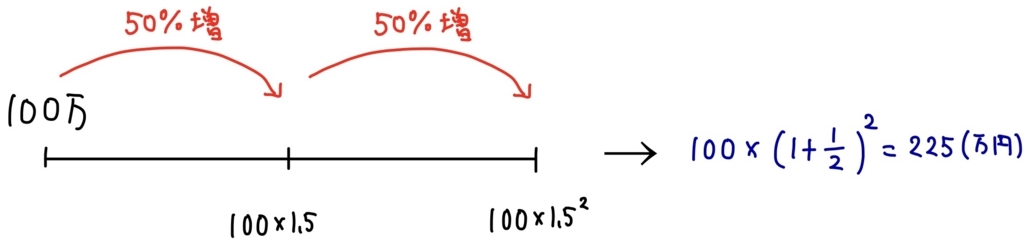
ここで100×1.5×1.5という計算が\( \displaystyle 100\times \left(1+\frac12 \right)^2 \)とかけることに注意しておきましょう。
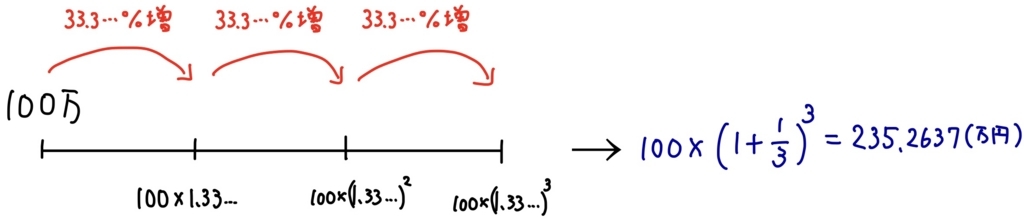
もっと儲けたい!と思ったあなたは今度は利息を\( \displaystyle \frac{1}{3} \)(約33.3%)にし、利息がかかるタイミングを3倍にしていきます(4ヶ月に33.3%の利息がつくことになる)。先ほどの計算と同様にして
\( \displaystyle 100\times\left(1+\frac13\right)^3=235.2637\cdots \)万円
という計算になります。先ほどの225万円よりもさらに増えている!
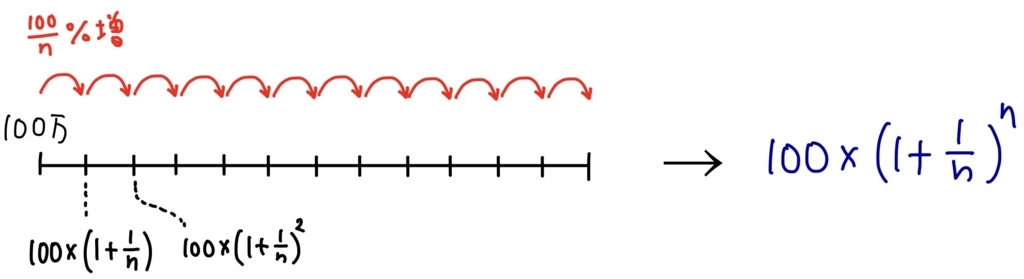
ここで文字を使って一般化しましょう。利息がかかる回数を\( n \)とすれば、あなたが得られる金額は上の計算と同様に考えれば
\( \displaystyle 100\times\left(1+\frac{1}{n}\right)^n \)万円
となることがわかります。
ここで\( \displaystyle \left(1+\frac{1}{n}\right)^n \)は\( n \)を大きくするときにいくらでも大きくなるのでしょうか。もしそうならば、利息を小さくする代わりに利息発生のタイミングを多くしていく、というあなたのビジネスは無限の儲けを得ることができそうです。しかし、実は、 \( \left(1+\frac{1}{n}\right)^n \)の値は\( n \)を大きくするごとに(つまり\( n\to\infty \)の極限を考えると)少しずつ増えてはいきますが、その値は
\( \displaystyle 2.71828182845904\cdots \)
という値に限りなく近づいていきます(有名な語呂合わせは「フナ一鉢二鉢一鉢二鉢しごくおいしい…」)。ですから利息がつくタイミングをどんなに多くしても272万円以上に増やすことはできないのです。
…ということで悪徳サラ金業者という設定でのお話をしましたが、実は上の定数\( 2.71828\cdots \)は、微分積分の計算でもよく登場する重要な定数なのです。これをネイピア数といい、\( e \)という記号で表します。
[box class=”blue_box” title=”ネイピア数\( e \)の定義”]\( \displaystyle e=\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n \)
[/box]
ではこの記事の後半戦ということで、上の極限が本当に収束するのかを証明してみましょう。高校の教科書にはあまり載っていません。
[box class=”blue_box” title=”本当に収束するのか”]
数列
\( \displaystyle a_{n}=\left(1+\frac{1}{n}\right)^n \)
は\( n\to\infty \)のとき収束する。
[/box][box class=”glay_box” ]
(解)「上に有界な単調増加数列は収束する」という事実を使う。
(ステップ1)数列\( \{a_n\} \)が単調増加であることを示す
二項定理で展開して見るとわかる。
\( \displaystyle a_n=\left(1+\frac{1}{n}\right)^n \)
\( \ \ \displaystyle =1\!+\!{}_nC_1\!\cdot\! 1^{n-1}\!\cdot\! \frac{1}{n}\!+\!{}_nC_2\!\cdot\! 1^{n-2}\!\cdot\!\frac{1}{n^2}\!+\!\cdots\)
\( \displaystyle \hspace{20mm} \cdots \!+\!{}_nC_r\!\cdot\! 1^{n-r}\!\cdot\! \frac{1}{n^r}\!+\!\cdots\! +\!{}_nC_n\!\cdot\! \frac{1}{n^n} \)
\(\ \ \displaystyle =\!1\!+\!1\!+\!\sum_{r=2}^{n}\frac{n(n-1)\cdots (n-r+1)}{r!}\cdot \frac{1}{n^r} \)
\( \ \ \displaystyle =1+1 \)
\( \displaystyle \hspace{7mm} +{\small \sum_{r=2}^{n}\frac{1}{r!}\left(1\!-\!\frac{1}{n}\right)\!\left(1\!-\!\frac{2}{n}\right)\!\cdots \!\left(1\!-\!\frac{r\!-\!1}{n}\right) }\) …①
(ここで\( \displaystyle n \)を\( \displaystyle n+1 \)に取り替えると)
\( \ \displaystyle a_{n+1}=1+1 \)
\( \displaystyle \hspace{4mm} +{\small \sum_{r=2}^{n+1}\!\frac{1}{r!}\left(\!1\!-\!\frac{1}{n\!+\!1\!}\right)\!\left(\!1\!-\!\frac{2}{n\!+\!1\!}\right)\!\cdots \!\left(\!1\!-\!\frac{r\!-\!1}{n\!+\!1}\!\right)}\!\) …②
①、②を見比べてみる。\( \sum \)の各項の因数について、\( \displaystyle 1\leq i\leq r-1 \)の各\( i \)で
\( \displaystyle \left(1-\frac{i}{n}\right)\lt \left(1-\frac{i}{n+1}\right) \)
であり、また②の方が項が1つ多い(どの項も正であることに注意)ことから\( a_n\lt a_{n+1} \)が文句なく成り立つ。すなわち数列\( \{a_n\} \)は単調増加する。
(ステップ2)数列\( \{a_n\} \)が上に有界であることを示す
①で\( \displaystyle 1\leq i\leq r-1 \)の各\( i \)で\( \displaystyle \frac{i}{n} \)を\( 0\)に取り替えた評価を考える。
\( \ \ \displaystyle a_n=1+1 \)
\( \displaystyle \hspace{7mm} +{\small \sum_{r=2}^{n}\frac{1}{r!}\left(1\!-\!\frac{1}{n}\right)\!\left(1\!-\!\frac{2}{n}\right)\!\cdots \!\left(1\!-\!\frac{r\!-\!1}{n}\right) }\)
\( \ \ \displaystyle \lt 1+1+\sum_{r=2}^{n}\frac{1}{r!} \)
(ここで\( r\geq 2 \)のとき\( r!=r(r-1)\cdots 2\cdot 1\gt 2^{r-1}\cdot 1=2^{r-1} \)が成り立つから)
\( \ \ \displaystyle \lt 1+1+\sum_{r=2}^{n}\frac{1}{2^{r-1}} \)
\( \ \ \displaystyle \to 1+1+\frac{\frac{1}{2}}{1-\frac12}=3 \ \ (n\to\infty) \)
よって任意の\( \displaystyle n \)で\( \displaystyle a_n<3 \)が成り立つから数列\( \{a_n\} \)は上に有界である。
(ステップ1)および(ステップ2)により、数列\( \{a_n\} \)は上に有界で単調増加なので収束する。(証明終)
[/box]二項係数を一般の文字で扱う処理は慣れていないと難しいかもしれませんね。では。
★★★
今回の内容の動画版です