今回の内容の動画版です→最小の材料で4点を結ぶ 早稲田大(教育)2015
西成活裕先生の『とんでもなく役に立つ数学』という本 に、数学3の微分積分のよさを感じられる面白い話題があります。2015年の早稲田大学の入試でこの話題が出題さているので、そちらから問題を持ってくることにします。
[box class=”blue_box” title=”問”]座標平面上に6点
\( A(1,1), B(1,-1), C(-1, 1), D(-1,-1)\),\( P(x, 0), Q(-x,0) \)(\( x>0 \))
をとる。このとき
\( \displaystyle AP+BP+PQ+CQ+DQ \)
が最小となるときの\( \displaystyle x \)を求めよ。
[/box]図にするとこんな感じ。
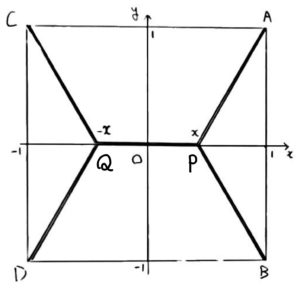
電気回路の配線だと思えば、A,B,C,Dをいかに少ない材料で結んでコストを減らすか?という問題と考えることもできますし、A,B,C,Dを都市と考えれば、それらを結ぶ道路を建設するのにいかに少ない建設費用で済ませるか、という問題と考えることもでき、リアルに繋がる面白い問題だと思います。
さて、この問題は直感的には道路をバッテンに結んだとき、すなわち\( \displaystyle x=0 \)のとき一番小さそうな気もしますが、実はそうではありません。実際に計算をしておきましょう。
[box class=”glay_box” title=”ラフな答案”]\( \displaystyle AP+BP+PQ+CQ+DQ =l\)とおくと,対称性から
\( \displaystyle \frac{l}{2}=OP+PA+PB \)
となる。

三平方の定理などから
\( \displaystyle \frac{l}{2}=x+2\sqrt{1+(1-x)^2} \)
となる。微分して
\( \displaystyle \frac{l’}{2}=1+\frac{-2(1-x)}{\sqrt{1+(1-x)^2}} \)
となる。\( \displaystyle \frac{l’}{2}=0 \)とおくと
\( \displaystyle \frac{1-x}{\sqrt{1+(1-x)^2}}=\frac12 \)
これを解いて
\( \displaystyle x=1-\frac{1}{\sqrt3}=0.42\cdots\)
(この点で最小値をとることは増減表などで確認できる)
[/box]なお、このときの道路の長さは
\( \displaystyle l=\left(1-\frac{1}{\sqrt3}\right)\cdot 2 +\frac{2}{\sqrt3}\cdot 4 \)
\( \displaystyle \ \ = 2+2\sqrt3 \)
です。一方、バッテンにしたときの道路\( AD+BC \)の長さは\( \displaystyle 4\sqrt2 \)ですから、最小となるときの道路との比は
\( \displaystyle \frac{2+2\sqrt3}{4\sqrt2}=\frac{\sqrt6+\sqrt2}{4}=0.9659\cdots \)
となります。つまり、最小にする道路はバッテン道路よりも約3.5%材料が少なくて済むことになっているのです。
では、これが本当に短くなっているということを納得するために、次の実験をしてみましょう。
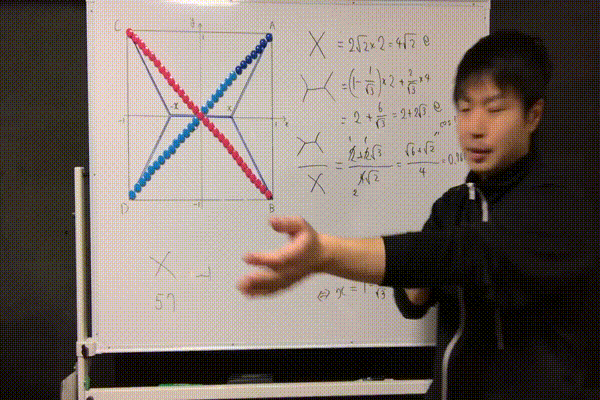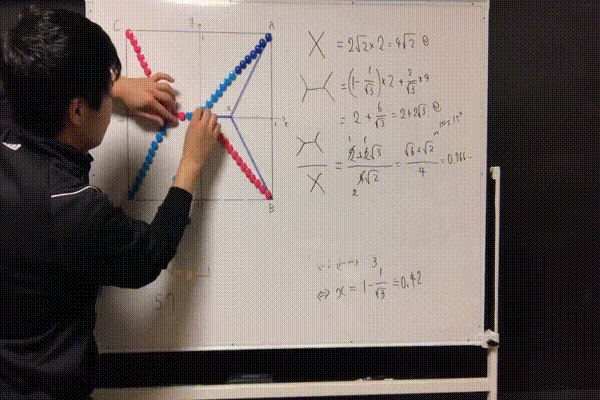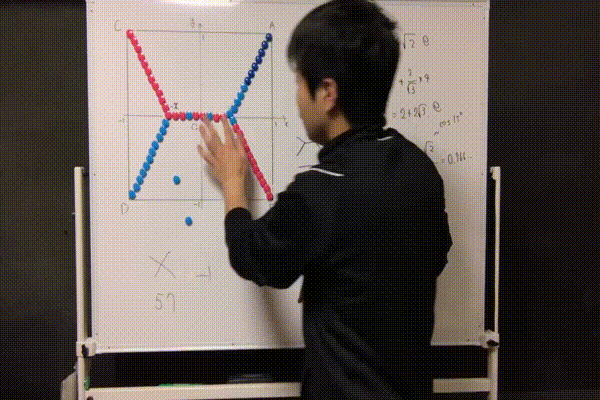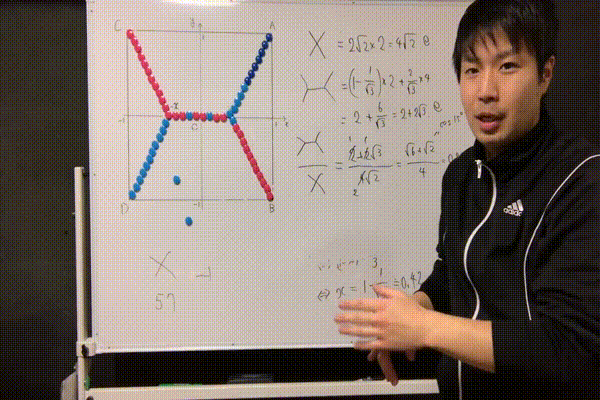
バッテンの道路では57個必要だったマグネットが、55個で済むようになっています。節約率は
\( \displaystyle \frac{55}{57}=0.9649\cdots \)
で先ほどの理論値\( \displaystyle \frac{\sqrt6+\sqrt2}{4}=0.9659\cdots \)と近い状況になっています。
(少し補足)
上の実験映像(GIF)は、節約率が理論値と近くなるようにマグネットの総数を設定しています。マグネット1個分が3.5%に相当するようにしようとすると、1÷0.035=28.57個のマグネットを用意…と整数値に近くない。そこでマグネット2個分が3.5%に相当するようにして2÷0.035=57.14≒57個のマグネットを用意しています。整数値に近く無い設定だと道路の”スキマ”が大きく、パフォーマンス的に少し微妙にりますのでご注意を。
今回はここまで!