今回は数学2の教科書に載っているこれ。
[box class=”blue_box” title=”点と直線の距離”]座標平面上で、点\( p(x_1, y_1) \)と直線\(\ l : ax+by+c=0 \)の距離\( d \)は
\( \ \ \displaystyle d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}} \)
で与えられる。
[/box]数学2の範囲でこれを証明しようとすると、かなりごちゃごちゃな計算をすることになります。そこで今回はベクトルを用いることにしましょう。
[box class=”glay_box” ](証明)
点\( P \)から直線\( l \)に下ろした垂線の足を\( P_0 \)とし、点\( P,P_0 \)の位置ベクトルをそれぞれ\( \displaystyle \vec{x_1},\vec{x_0} \)とする。また、直線\( l \)の法線ベクトルを\( \displaystyle \vec{n} \)とする。
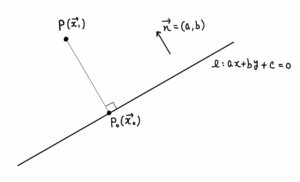
\( \displaystyle \vec{x_1}-\vec{x_0} \)は\( \displaystyle \vec{n} \)と平行なので
\(\ \ \displaystyle \vec{x_1}-\vec{x_0}=t\vec{n} \) …①
となる\( t \)が存在する。いま我々が知りたいのはこの右辺のベクトルの大きさ\( \displaystyle d=|t\vec{n}| \)であることに注意しよう。その目的のためには\( t \)を求めなくてはならない。①の両辺に\( \displaystyle \vec{n} \)との内積をとってみよう。\( \displaystyle \vec{x_0} \)が\( l \)上の点で\( \displaystyle \vec{n}\cdot\vec{x_0}=-c \)となることから
\( \ \ \displaystyle \vec{n}\cdot \vec{x_1}+c=t|\vec{n}|^2 \)
すなわち
\(\ \ \displaystyle t=\frac{\vec{n}\cdot \vec{x_1}+c}{|\vec{n}|^2} \)
となる。よって
\(\ \ \displaystyle d=|t\vec{n}|=\frac{|\vec{n}\cdot \vec{x_1}+c|}{|\vec{n}|^2}|\vec{n}| \)
\( \ \ \displaystyle =\frac{|\vec{n}\cdot \vec{x_1}+c|}{|\vec{n}|} =\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}} \)
となり、目標の公式を得る。(証明終)
[/box]ベクトルの設定、直交の関係を確認する最初の段階だけ図で確認しますが、一度設定が終わったらあとは機械的な計算に持ち込んで処理しています。これがベクトルの良さですね。
ところで、数研出版数学Bの教科書の研究のページに同様の内容があるのですが、最後までベクトル使えばいいのに、なぜか途中から座標に戻してるんですよね…
[kanren postid=”93,92,67″]今回はこの辺で。