教員向けの記事です。
今回はレーザー測定器を教材としても使えそう!という内容をまとめます。
アマゾンなどで「レーザー 測定器」と調べるといろいろなメーカーから、安いものだと3000円台ぐらいから発売されています。(以下、実際に使っていたものが生産停止になっていたので、同様の商品をはっておきます。2020年3月15日追記)
学校現場では体育館やグラウンド、教室などで距離を測定する場面がたまーにあります。体育準備室からメジャーをガラガラ持ってこなくても、これでできるんです。便利ですよー
値段も数千円とお手頃なので購入を検討してみてはいかがでしょうか。
さて、本題はこの測定器が三平方の定理の説明で使える、ということです。
ここで一応述べておくと、三平方の定理というのは、斜辺\( \displaystyle c\),他の2辺 \( \displaystyle a,b \)の直角三角形において
\( \displaystyle a^2+b^2=c^2 \)
が成り立つ、というものでした。このことから、”3辺のうち2辺がわかれば、残りの1辺は計算できる”ということがわかります。
三平方の定理は中学3年生で学ぶ内容なわけですが、この定理に親近感というか、使いこなせた感が持てない生徒も多いでしょう。今回の方法によって、そうした生徒向けに三平方の定理の良さを実感させることができるかもしれません。
黒板上に長さを図りたいものがあるのですが、いろいろな理由で近づくことができないと場面設定します。例えばそこに崖があって、近づけないなどとするとよいでしょう。(下図は、黒板に貼られた紙の上下の長さを計測しようとしている様子です)

このとき、
①計測地点から測りたいもの(紙)の上端
②計測地点から測りたいもの(紙)の下端
③壁までの水平距離
の3つの距離を測定します(以下写真参考)。
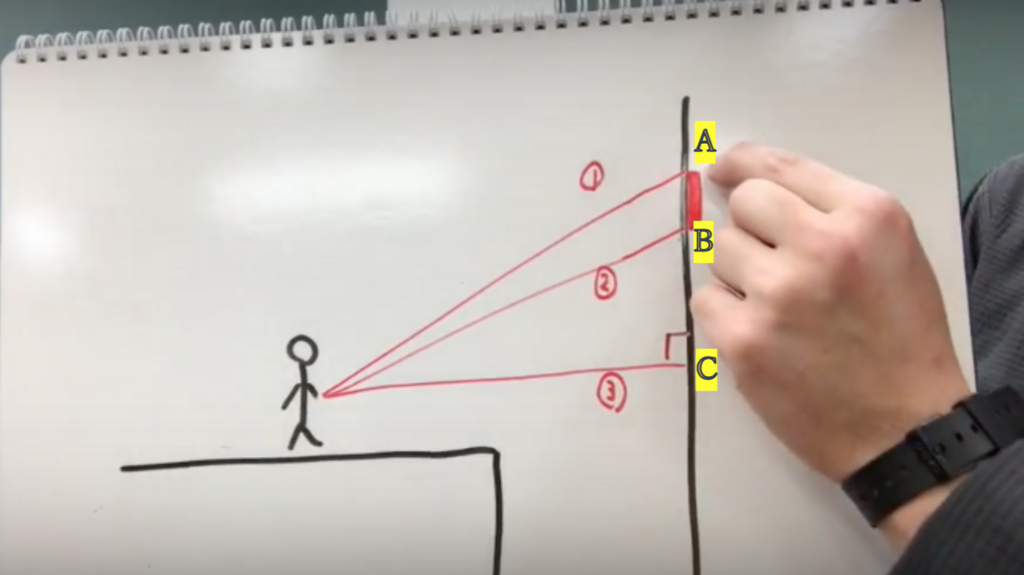
①〜③の距離情報があれば、三平方の定理によって図りたいものの長さ(上写真のAB)を計算することが理論上可能です。
実際、上図の①と③の長さから、(測定地点,A,Cを頂点とする直角三角形の)三平方の定理よりACが計算でき、また上図の②と③の長さから(測定地点, B,Cを頂点とする直角三角形の)三平方の定理でBCが計算できます。
よってACからBCを引けば物体の長さABが計算できることになるのです。このような計算はピタゴラス計算(三平方の定理の別名がピタゴラスの定理ですね)とよばれ、この測定器の中にも組み込まれています。下写真は①、②、③の測定結果(1.224, 1.083, 0.882)から紙の長さ(0.220m)が自動計算されたところのものです。

ちなみに計測した紙はA4用紙の短いところの長さで、実際の長さは21cm(=0.210m)。上の計測結果は教室での実演目的に十分な精度だといえます。
是非お試しください〜〜
今回の記事は以下の動画から作成しています。
レーザー測定器で、三平方の定理を使う
今回はここまでです