動画や音楽などのデータには通常、符号理論というものが使われています。符号理論を使うことで、多少のノイズなどが入ってしまったようなデータであっても、数学的な計算によって元のデータに戻すことができます。このことを実感する題材としては、QRコードがよいでしょう。QRコードは、マジックなどで黒く汚しても、多少の汚れであれば正確な読み込みに勝手に訂正してくれます。これは「誤り訂正符号」という数学的な工夫があるからできることなのです。今回はこの概要をお話です。
よく知られているように、デジタルデータは究極的には0と1の文字列で表すことができます。どんな長さのデータであっても、細かく区切ってしまえば長さの短い文字列の集まりと考えることができますから、今回は4桁の文字列を考えることにしましょう。例えば
(0101)
というデータがあったとします。このデータを誰かの元へ届ける際に、何らかの理由でノイズが入り、データが次のように変わってしまったとしましょう。
(1101)
データを受け取った側から見ると、このデータがノイズ入ってこうなってしまったのか、それとも元からこのようなデータであったのかの判断ができません。
そこで、ノイズが入ったかどうかをチェックできるように、桁数を追加します。
いま考えている4桁の文字列は合計\( 2^4=16 \)種類あります。これにそれぞれ3つずつ桁を追加し、次のように7桁の文字列を考えます。
\( c_0= \)0000000、\( c_1= \)1000111
\( c_2= \)0100101、\( c_3= \)0010010
\( c_4= \)0001001、\( c_5= \)1100010
\( c_6= \)1010101、\( c_7= \)1001110
\( c_8= \)0110111、\( c_9= \)0101100
\( c_{10}= \)0011011、\( c_{11}= \)1110000
\( c_{12}= \)1101011、\( c_{13}= \)1011100
\( c_{14}= \)0111110、\( c_{15}= \)1111000
これらの”数字が並んだもの”は通常,ベクトルとよばれます。この場合は各成分が0か1の7桁(7次)のベクトルです。(登場する”数字”が0と1だけなので体(たい)\( F=\{0,1\} \)上のベクトルとよばれます)。ベクトルには足し算や定数(スカラー)倍などの計算が定義されています。今回は足し算や定数倍(とはいっても0倍と1倍しかありませんが)はそれぞれの桁ごとに行う、という規則で定義しています(なお、この16個の中だけで演算が閉じているのでこの集合\( C=\{c_0, c_1, \cdots , c_{15}\}\)は7次のベクトル空間の部分集合、すなわち部分ベクトル空間などといいます。詳しくは下部の(補足)で)。
3桁の追加により、上の文字列\( c_0, c_1, \cdots , c_{15} \)は7桁のベクトルに”格上げ”されました。これによって、文字列\( c_0, c_1, \cdots , c_{15} \)が7桁のベクトルの集合の中にポツンポツンと存在する立場になるわけです。心の中では、下図の赤に相当するようなイメージを持っておくとよいでしょう。

このポツンポツンと存在していることがノイズチェックをする上で有効です。
ベクトル間の”距離”は、各成分のうち一致していない桁の個数と定義され、”ハミング距離”と呼ばれます。
[box class=”blue_box” title=”ハミング距離”]体\( F=\{0,1\} \)上の\( n \)次元ベクトル\( x,y \)に対し、そのハミング距離\( d(x,y) \)を
\( d(x,y) =\)(対応する位置にある異なった桁の個数)
と定義する。
[/box]
例えば
\( c_2= \)0100101
\( c_3= \)0010010
は左から2桁目、3桁目、5桁目、6桁目、7桁目の5箇所が異なっているので
\( d(c_2, c_3)=5 \)
となります。
さて、上の例の7桁の文字列\( c_0, c_1, \cdots , c_{15} \)のハミング距離の最小値は3となっています(どのように計算するかは下補足参照)。つまり、何か一つ\( c_i \)を選んだときに、それらの桁を少なくとも3個改変しないと別の文字列\( c_j (j\not= i) \)にはならないわけです。そこで、ノイズが入るなどして元データと変わってしまった桁が1つ以下と仮定すれば、ベクトルを受け取ったとき、ハミング距離が最も近い(1以下の)符号語がただ一つ決まりますから、それが元のデータだと推測できることになります。
例えば符号語
\( c_9= \)(0101100)
でどこか一箇所の成分が変わったベクトルは次の8通り
\( c_9+ \)+(1000000)=(1101100)
\( c_9+ \)+(0100000)=(0001100)
\( \vdots \)
\( c_9+ \)+(0000001)=(0101101)
あるわけですが、これらはすべて\( c_9 \)とのハミング距離が1で、また\( c_9 \)以外の符号語とのハミング距離は2以上です。このことから元々は符号語\( c_9 \)だったのだろう、と決定(=誤り訂正)できるのです。次図はその雰囲気を表現したもの。
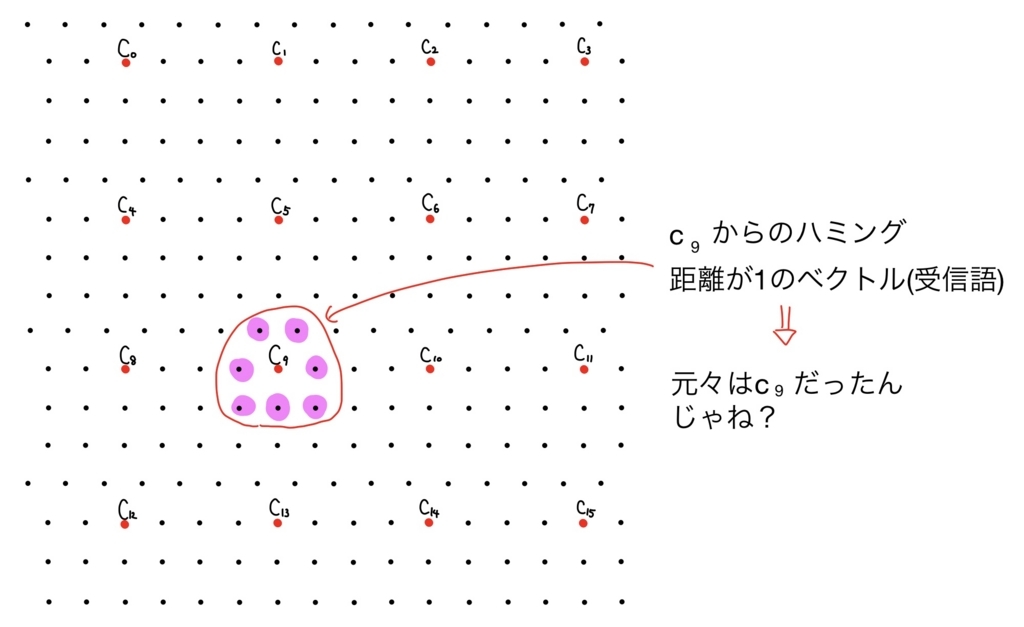
以上のように、情報に多少のノイズが含まれても、多少であれば元に戻すことができるようにした技術が「符号理論」と呼ばれる分野の「誤り訂正符号」というものです。我々がYouTubeで安定して動画が見られるのも!ケータイ電話で通話ができるのも!こうした符号理論の技術があるからなんですね!
今回はベクトル空間の定義もろくに言わずに符号理論の概要だけを紹介しました。実際には
・4次元の情報を7次元の符号語にするとき
・受け取ったベクトルが符号語からどれぐらいずれているか
などは行列計算を行いますし、直交補空間の次元など線形代数の理論についての知識があると理解しやすい話題です。高校生に話をする際には大学の数学をきちんと勉強するとそうしたこともわかるようになるぞーなどと伝えてもいいかもしれませんね。
(補足)
今回の文字列の集合\( c_0, c_1, \cdots , c_{15} \)は\( c_1, c_2, c_3, c_4 \)を基底とする4次元の(部分)ベクトル空間です。
(再掲)
\( c_0= \)0000000、\( c_1= \)1000111
\( c_2= \)0100101、\( c_3= \)0010010
\( c_4= \)0001001、\( c_5= \)1100010
\( c_6= \)1010101、\( c_7= \)1001110
\( c_8= \)0110111、\( c_9= \)0101100
\( c_{10}= \)0011011、\( c_{11}= \)1110000
\( c_{12}= \)1101011、\( c_{13}= \)1011100
\( c_{14}= \)0111110、\( c_{15}= \)1111000
\( c_1, c_2, c_3, c_4 \)が基底になっていることと文字列が和に関して閉じていることは次のような規則からわかります(二元体\( F=\{0,1\} \)の性質上、同じベクトルを足すと\( c_0=\)(0000000)(ゼロベクトル)になるということに注意するとよいです)
<基底2つの和>
\( c_1+c_2=c_5, \ c_1+c_3=c_6, \ c_1+c_4=c_7, \)
\( c_2+c_3=c_8,\ c_2+c_4=c_9,\ c_3+c_4=c_{10} \)
<基底3つの和>
\( c_1+c_2+c_3=c_{11}, \ c_1+c_2+c_4=c_{12} \)
\( c_1+c_3+c_4=c_{13},\ c_2+c_3+c_4=c_{14} \)
<基底4つの和>
\( c_1+c_2+c_3+c_4=c_{15} \)
「集合\( C \)が(部分)ベクトル空間だと何が嬉しいの?」と思われる方もいらっしゃるかもしれませんが、\( C \)がベクトル空間である場合、
「ハミング距離の最小値\( d=\min\{d(c_i,c_j)|c_i,c_j\in C\ , i\not= j\} \)」
が
「非零である桁の個数の最小値\( d’=\min\{c_l|c_l\in C, c_l \not=c_0 \} \)」
と等しいことがわかります。
実際、ハミング距離の最小値\( d=d(c_m,c_n) \)を与えるようなベクトルの組\( c_m, c_n\in C (i\not= j)\) に対して,\( C \)は減法で閉じています(-1倍を足す計算だから)。すなわちその差\( c=c_m-c_n \)が\( C \)に属することになり、しかも\( c\not= c_0 \)です。よって\( d’ \)が\( C \)における0ベクトル\( c_0 \)を除く非零である桁の個数の最小値であるという定義から\( d\geq d’ \)が成立します。一方、0でない桁の個数が最も小さいようなベクトル(ただし0ベクトル\( c_0 \)は除く)を\( c_l \)とすれば\( d’=d(c_l,c_0) \)であり、\( d \)がハミング距離の最小値であることから\( d\leq d’ \)が得られます。\( d\geq d’ \)かつ\( d\leq d’ \)なのだから\( d=d’ \)となります。
上の記事の説明の中で\( C \)のハミング距離の最小値が3であるとサラッとかいてありますが((下補足参照)と書いた部分)、それは一瞬ではわかりにくいはず。しかし「0ベクトル以外で非零である桁の個数」として考えれば簡単に3であることがわかるのです。この一例でも察せされるように、文字列の集合\( C \)が(部分)ベクトル空間であることは、線型代数のいろいろな道具を援用することができるので、運用上いろいろと都合がよいのです。
(参考)
J.ユステセン, T.ホーホルト, (訳)阪田省二郎,栗原正純,松井一,藤沢匡哉『誤り訂正符号入門』