2018年10月〜2019年6月に公開した272本の動画全リストです。
もくじ
パズルっぽいもの(計算系) 11本
| 大きいのはどっち?【1分間クイズ】
大きいのはどっち? \( \displaystyle \frac{12345}{20190412} \) \( \displaystyle \frac{12346}{20190413} \) コメント欄、大変勉強になりました.(19/4/12up) |
| 中学入試の最初によくある計算【1分間クイズ】
次の式を計算せよ. \( \displaystyle 4\times 4\times 3.34-33.4\times 0.75+0.167\times 30 \) (19/4/10up) |
| 2^320+2320が56の倍数であることを示せ【1分間クイズ】
\( \displaystyle P=2^{320}+2320 \) が56の倍数であることを示せ.(19/4/6) |
| 3文字の連立方程式【1分間クイズ】
次を満たす正の数\( \displaystyle x,y,z \)を求めよ. \( \displaystyle \begin{cases}x(y+z)=25\\y(z+x)=16\\z(x+y)=21\end{cases} \) (19/4/5up) |
| 10桁の整数2019a0323bが72の倍数のときa, bは?【1分間クイズ】
この日はとあるアイドルの方の誕生日だったようです.(19/3/23up) |
| 一番大きいのは?【1分間クイズ】
一番大きいのはどれ? \( \displaystyle \sqrt3,\ \ \sqrt[3]{5},\ \ \sqrt[4]{10} \) ふつうの方法で比較します.(19/3/21up) |
| √(n^2+23)が整数となる自然数nは?【1分間クイズ】
\( \displaystyle \sqrt{n^2+23} \) が整数となるような自然数\( \displaystyle n \)は? 当初は自然数という条件を表記していなかったのでいろいろと議論となった動画です.(19/3/17up) |
| (1!)(2!)…(12!)をある(k!)で割って平方数にせよ【1分間クイズ】
解説がまったく1分で収まってない動画です.(19/3/17up) |
| 方程式の合成【1分間クイズ】
\( \displaystyle f(x)=x^2+4x+2 \)とする. 方程式\( \displaystyle f(f(f(x)))=0 \)の実数解を求めよ. (19/3/14up) |
| √111556 = ? 【1分間クイズ】
\( \displaystyle \sqrt{111556}\) を変態的な式変形で計算しました.(19/3/14up) |
| どっちが大きいか?【1分間クイズ】
大きいのはどっち? \( \displaystyle 333\times 444 \ \ 222\times 667\) (19/3/11up) |
パズルっぽいもの(図形系) 27本
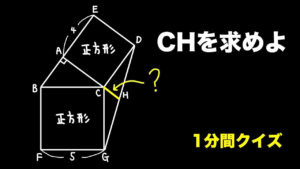
| 直角三角形に付いた2つの正方形が作る線分【1分間クイズ】
うまく処理してみてください。(19/5/30up) |
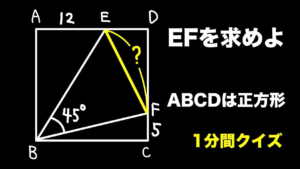
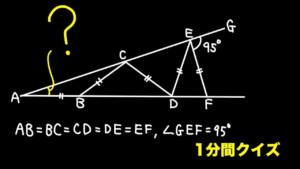
| 辺の長さは?【1分間クイズ】
直角に注目すれば… (19/5/29up) |
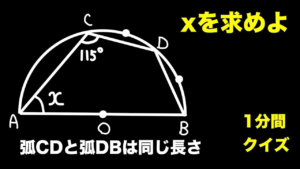
| 半円がらみの角度を求めよ【1分間クイズ】
同じ弧の大きさということから… (19/5/28up) |
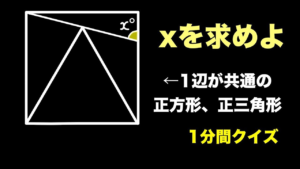
| 角度を求めよ【1分間クイズ】
単純な図形ですが、どうでしょう。(19/5/27up) |
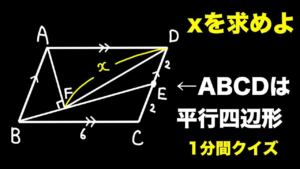
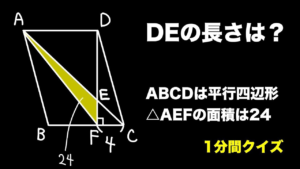
| 平行四辺形内部の線分の長さ【1分間クイズ】
最初の1手は大体きまっていますが…(19/5/25up) |
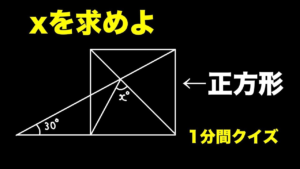
| 正方形を横切る直線と対角線の交点が作る角の大きさ【1分間クイズ】
対角線ですから…(19/5/25up) |
| 角度の合計は?【1分間クイズ】
合計がわかればよいので…(19/5/23) |
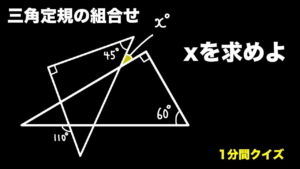
| 三角定規を組合わせた角度【1分間クイズ】
単純な問題ですが,ちょっと考えるかもしれません.(19/5/22up) |
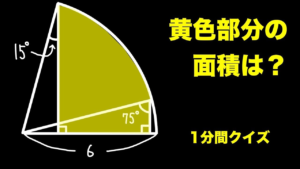
| 扇型を縦に切った領域の面積【1分間クイズ】
一回計算ミスしたので再アップした動画です.(19/5/22up) |
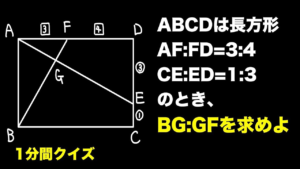
| 辺の比を求める【1分間クイズ】
Eに注目したくなります…(19/5/20up) |
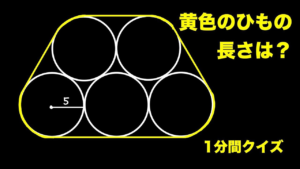
| 円を束ねたときのひもの長さ【1分間クイズ】
筒を輪ゴムで束ねた感じですね.(19/5/19up) |
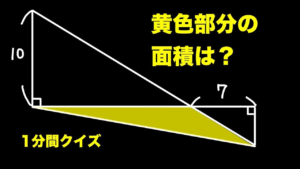
| 面積を求める【1分間クイズ】
等積変形など使える変形はどんどん使いましょう.(19/5/14up) |
| 長さを求める【1分間クイズ】
同じ面積をもつ場所がないかなど考えましょう.(19/5/14up) |
| 角度を求めよ【1分間クイズ】
求まると気持ちいいです.(19/5/13) |
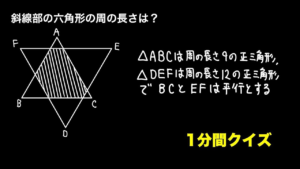
| 斜線部六角形の周の長さ【1分間クイズ】
見方を柔軟にするとスグわかります.(19/5/9up) |
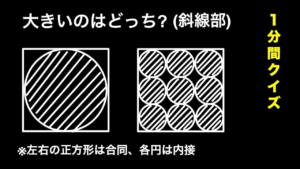
| 大きいのはどっち?【1分間クイズ】
直感と計算結果が同じでしょうか.(19/4/7up) |
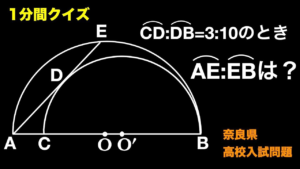
| 弧の長さの比【1分間クイズ】
弧の比をどう処理するかが大切です.(19/3/31up) |
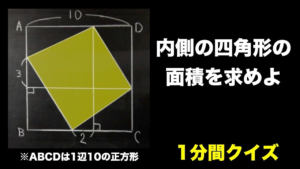
| 内側の四角形の面積【1分間クイズ】
うまく処理しましょう.(19/3/26up) |
| 内側にある平行四辺形の面積の割合は?【1分間クイズ】
いい問題です.(19/3/24up) |
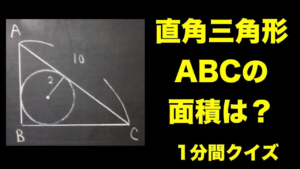
| 直角三角形の面積【1分間クイズ】
普通に計算です.(19/3/21up) |
| トゲトゲした図形の面積【1分間クイズ】
まずトゲトゲを処理しましょう.(19/3/19up) |
| 長方形の個数は?【1分間クイズ】
解法が面白すぎる!(19/3/14up) |
| 角度の合計は?【1分間クイズ】
合計がわかればよいので…(19/3/12up) |
| 四角形に内接する2円の半径の和【1分間クイズ】
(19/3/10up) |
| とがった7箇所の角度の合計【1分間クイズ】
うまく処理していきましょう.(19/3/10up) |
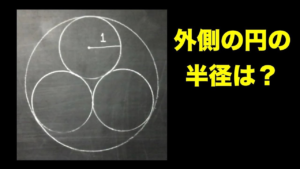
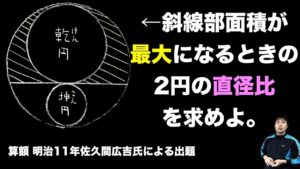
| 3つの円が内側で内接している円の半径【1分間クイズ】
算額とかでありそう.(19/3/9up) |
| 1本の直線で面積を2等分せよ【1分間クイズ】
定規は使ってOKですが長さをはかったり,角度をはかったりするのはダメとします.(19/3/8up) |
高校数学演習 15本
| 三角関数のグラフがつくる領域面積を二等分する【高校数学演習】
曲線\( \displaystyle y=\cos x \) \( \displaystyle \left( 0≦x≦\frac{\pi}{2} \right)\)と\( \displaystyle x \)軸,\( \displaystyle y \)軸で囲まれる領域の面積を,\( \displaystyle y=a\sin x \)が2等分するような正の定数\( \displaystyle a \)の値を求めよ.(19/6/8up) |
| 定積分漸化式3つ【高校数学演習】
3つの定積分漸化式を導く. \( \displaystyle \gamma_n=\int_{0}^{1}x^ne^{-x}dx \) \( \displaystyle I(m,n)=\int_{0}^{1}x^m(1-x)^{n}dx \) \( \displaystyle I_n=\int_{0}^{\pi}\sin^nxdx \) (19/6/7up) |
| 周期性を利用した三角関数の積分【高校数学演習】
\( \displaystyle I=\int_{0}^{n\pi}\left|\sin x+\cos x\right|dx \)の計算.(19/6/3up) |
| 三角関数の積の積分【高校数学演習】
(1) \( \displaystyle m,n \)を整数とするとき \( \displaystyle I=\int_{0}^{\pi}\sin mx\sin nx dx \) を計算せよ. (2) 自然数\( \displaystyle n \)に対し \( \displaystyle f_n(x)=\sin x+\sin 2x+\cdots +\sin nx \) とおくとき,次の積分を計算せよ. \( \displaystyle J=\int_{0}^{\pi}\left\{f_n(x)\right\}^2 \)dx (19/5/30up) |
| 絶対値が入った積分の処理【高校数学演習】
\( \displaystyle f(x)=\int_{0}^{1}|t^2-x|dt \) \( \displaystyle (0<x<1) \) の最小値を求めよ.(19/5/29up) |
| 無限積の処理【高校数学演習】
(1) \( \displaystyle x>0 \)のとき次を示せ. \( \displaystyle x-x^2<\log (x+1)< x \) (2) 自然数\( \displaystyle n \)に対し \( \displaystyle A_n=\left(1\!+\!\frac{1}{n^2}\right)\!\left(1\!+\!\frac{2}{n^2}\right)\!\left(1\!+\!\frac{3}{n^2}\cdots\right)\) \( \displaystyle \hspace{9em}\cdots\!\left(1\!+\!\frac{n}{n^2}\right) \) と定める.\( \displaystyle \lim_{n\to\infty}A_n \)を求めよ.(19/5/27up) |
| √5の√7乗と√7の√5乗はどっちが大きい?【高校数学演習】
有名問題です.(19/5/26up) |
| 正n角形に関する不等式【高校数学演習】
\( \displaystyle n \)を3以上の整数とする.辺の長さの和が\( \displaystyle 2\pi \)である正\( \displaystyle n \)角形の面積を\( \displaystyle S_n \)とする. (1) \( \displaystyle S_n \)を\( \displaystyle n \)の式で表せ. (2) \( \displaystyle S_{n+1}>S_n \)を示せ. (3) \( \displaystyle \lim_{n\to \infty} S_n \)を求めよ. (19/5/26up) |
| 不等式が常に成り立つための定数aの条件【高校数学演習】
\( \displaystyle n \)を自然数とする.すべての正の数\( \displaystyle x \)に対して \( \displaystyle \log x+\frac{a}{x^n} >0\) が成立するための実数\( \displaystyle a \)の値の範囲を\( \displaystyle n \)を用いて表せ. (19/5/23up) |
| 関数方程式【高校数学演習】
微分可能な関数\( \displaystyle f(x) \)が次の2条件を満たすとする. ・任意の\( \displaystyle x,y \)で \( \displaystyle f(x+y)=f(x)+f(y)+2xy \) ・\( \displaystyle f'(0)=1 \) このとき,次のものを求めよ. (1) \( \displaystyle f(0) \) (2) \( \displaystyle f'(x) \) (19/5/23up) |
| 多変数関数の最大値【高校数学演習】
\( \displaystyle x+y+z=\pi, x>0, y>0, z>0 \)のとき \( \displaystyle \sin x\sin y\sin z \) の最大値と,最大値を与える\( \displaystyle x,y,z \)の値を求めよ. 実質2変数関数の最大値ですので,予選決勝法を使って示しました.(19/5/21up) |
| 極小値をもつための条件【高校数学演習】
関数 \( \displaystyle f(x)=\frac{x^2+k}{e^x} \) が極小値をもつための\( \displaystyle k \)の条件を求めよ.(19/5/18up) |
| 1の無限乗の処理【高校数学演習】
次の極限を求めよ. (1) \( \displaystyle \lim_{x\to\infty}\left(1+\frac{3}{x+1}\right)^x \) (2) \( \displaystyle \lim_{x\to 0} (1-2x)^{\frac{1}{x}}\) (19/5/14up) |
| 曲率半径の計算【高校数学演習】
\( \displaystyle k \)を正の定数とする.曲線\( \displaystyle y=\cos kx \)と3直線\( \displaystyle x=-\theta, \)\( \displaystyle x=0, \)\( \displaystyle x=\theta \) (\( \displaystyle 0<\theta<\frac{2\pi}{k} \))との交点を通る円の中心を\( \displaystyle \text{P} \)とする.\( \displaystyle \theta \) が\( \displaystyle 0 \)に近づいていくとき,\( \displaystyle \text{P} \)はどのような点に近づくか. (19/5/11up) |
| 多項式・指数関数・階乗の比の極限【高校数学演習】
次の数列の極限を求めよ. (1) \( \displaystyle \lim_{n\to\infty}\frac{n^2+3n}{2^n} \) (2) \( \displaystyle \lim_{n\to \infty}\frac{3^n}{n!} \) (19/5/8up) |
主に中学〜高校範囲のネタ 104本
| 偶関数の積分を難しく表す一見簡単そうな積分を難しく表す話です.以下のことを示します.
\( \displaystyle f(x) \)を偶関数とするとき \( \displaystyle \int_{R}^{R}\frac{f(x)}{a^x+1}dx=\int_{0}^{R}f(x)dx \) が成立する.(19/6/6up) |
| 平行な3線分の関係【調和平均】
平行線の中に\( \displaystyle a, b \)の調和平均の半分\( \displaystyle \left(\frac{1}{a}+\frac{1}{b}\right)^{-1} \)が現れている.(19/6/5up)
|
| 対数積分の評価
\( \displaystyle \lim_{x\to\infty}\frac{1}{x}\int_{2}^{x}\frac{dt}{\log t}=0 \)を示す.積分区間を\( \displaystyle \sqrt{x} \)で分けるのがコツ.ロピタルの定理でもOK.(19/5/31up) |
| 増加・減少は区間に対して使う言葉です
関数\( \displaystyle f(x) \)が区間\( \displaystyle I \)で増加するということの定義、正確にいうことができますか?定義をしっかりとおさえる重要性が感じられる話題です.(19/5/21up) |
| 角θが入った式の評価
\( \displaystyle 0<\theta<\frac{\pi}{2} \)とする. \( \displaystyle \sin\theta<\theta<\tan\theta \)を利用して \( \displaystyle \frac{1}{\sin\theta}-\frac{1}{\theta}<1 \)を示せ. 簡単そうに見えますが…(19/5/18up) |
| 紙を何回折ると月に届くか計算してみた
昔から何度も聞いているネタですがYouTubeで計算をしている人があまりいなかったのでやってみました.結果を覚えているよりもその導く過程が大事ですね.(19/5/15up) |
| 行き先が指定されたあみだくじの作り方
先にスタートとゴールが決められたくじをどのように構成するのか、その具体的な手順です.意外にもネット上で解説されているものが見つからなかったので解説してみました.(19/5/14up) |
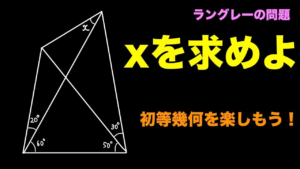
| 角度を求めよ【ラングレーの問題】
数学Aで時間が余ったときに使えるネタです.なかなか手強い.(19/5/12) |
| 偽物コインが入った袋を1回の計測で判定する
3つのコイン袋A, B, Cのうち,1つの袋だけ偽物のコインからなるとする.本物のコインが1枚10g, 偽物のコインが1枚9gであるとき,重さが計測できるはかりを1回だけ使って偽物の袋を見つけるにはどうすればよいか. 視聴者さんからオススメされた漫画を読んでみました.(19/5/12) |
| ローン返済額の公式年利6%の利率で100万円のローンを組む.毎月利息分と合わせて同じ金額を返していく方式(元利金等返済)で5年(60ヶ月)で完済するとき,毎月の返済額はいくらか.
等比数列の和公式を使った実用的な公式を導きます.(19/5/12up) |
| 自然数の和、自然数の二乗の和公式を図形的に導く
\( \displaystyle 1+2+3+\cdots +n=\frac{1}{2}n(n+1) \) \( \displaystyle 1^2+2^2+3^2+\cdots +n^2\) \( \displaystyle \hspace{7em}=\frac{1}{6}n(n+1)(2n+1) \) を図形的に導きます.(19/5/9) |
| 二項定理を使って指数関数から多項式を取り出す計算
\( \displaystyle a>1 \)のとき \( \displaystyle \frac{n}{a^n}\to 0 (n\to \infty) \) を示します.(19/4/13up) |
| 二重根号【1分間クイズ】
\( \displaystyle \sqrt{6-\sqrt{49-\sqrt{192}}} \)を簡単にせよ. (19/4/10up) |
| 原因の確率って、図で考えた方が見通し良くないですか?【ベイズの定理】
ある製品を製造する工場A, Bがあり,Aの製品には3%,Bの製品には4%の不良品が含まれている.Aの製品とBの製品を,4:5の割合で混ぜた大量の製品の中から1個を取り出すとき,次の確率を求めよ. (1) それが不良品である確率 (2) 不良品であったときに,それがAの製品である確率 図を使ってまとめ,図から確率を計算する方法を述べました.参考書とかのように文字ベースで導くやり方は私にはできません.(19/4/8up) |
| バーコードの秘密
チェック・デジットについての話です.(19/4/5up) |
| ベクトルで淡々とcosθを計算する
図形をみて初期設定がすんだらあとは機械的な計算をやればOKというベクトルの雰囲気を語りました.(19/4/3up) |
| オイラーの定数ガンマ【教員採用試験 千葉県】
\( \displaystyle a_n=1+\frac12+\frac13+\cdots+\frac{1}{n}-\log n \)とおく. (1) 自然数\( \displaystyle n \)に対し\( \displaystyle a_n>0 \)を示せ. (2) 数列\( \displaystyle \{a_n\} \)は単調減少であることを示せ. |
| スーパーかけ算九九 正負の数の乗法
負の数同士の積が正になることの説明など.(19/4/3)up |
| コラッツ数列 コラッツ予想 今年の自由研究はこれで決まりだ!
偶数なら次の項は半分に,奇数なら次の項は3倍して1を足すというルールで作られるのがコラッツ数列です.「どんな初項からはじめても,コラッツ数列はいつか1に達する」というコラッツ予想は証明ができていない未解決問題です.(19/4/2up) |
| 三平方の定理 証明
三平方の定理を編集を入れて証明してみました.(19/4/1up) |
| 微分とは何か?【中学生向け】
はじめての生徒にはこんな感じで概要を教えるかも.実際に接線の傾きを読み取らせるのが大事な気がしています.(19/3/30up) |
| 2桁以上のレピュニット数11…1は平方数にはならない
もちろん背理法です.(19/3/29up) |
| 角の二等分線の長さ
編集を使うのにハマり始めたころです.(19/3/28up) |
| 中線定理
三平方の定理を繰り返し使います.(19/3/28up) |
| ピックの定理【修正版】
格子多角形の面積を一瞬で計算する公式の利用の仕方と,なぜ成り立つのかを直感的に解説.(19/3/26up) |
| 平方数の和【教員採用試験 新潟県】
次の問に答えよ. \( \displaystyle z=a+bi, w=c+di \) (\( \displaystyle a,b,c,d \)は実数,\( \displaystyle i \)は虚数単位)のとき,\( \displaystyle |z|^2|w|^2=|zw|^2 \)を示せ. (2) \( \displaystyle 58\times 136 \)を平方数の和で表せ. (19/3/24up) |
| 手品しまーす
順番をぐちゃぐちゃにした紙の並びを,機械的な処理でもとの順番に並び替える手品!(19/3/23up) |
| トレミーの定理 証明
初等的にやるには巧みな補助線が必要です.(19/3/21) |
| こんなところにルートが!【パスタメジャー】
パスタを図るグッズの穴の半径に平方根の考えが使われているという話です.(19/3/20up) |
| 1が並んだ11…1の形の素数について【未解決問題】
レピュニット素数が無限にあるかどうかは未解決です.(19/3/18up) |
| (cos kθ)^2の和【教員採用試験 岩手県】
誘導が面白い!(19/3/14up) |
| 「気温のグラフ」で考える二次不等式
苦手な生徒を想定した導入方法です.知っているもので置き換えるとわかりやすいかもです.(19/3/14up) |
| ニュートン法【数値計算】
数値計算で使われるニュートン法の, \( \displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f'(x_{n})} \) という形の漸化式を導きます.(19/3/11up) |
| (sinθ-1)/(cosθ-√3)の最大最小【教員採用試験 香川県】
\( \displaystyle \frac{\sin\theta-1}{\cos\theta-\sqrt3} \) の最大値最小値について (1) 微分法による解答を示せ. (2) 微分法以外の分野で指導する場合の解答を示せ. (19/3/10up) |
| ネイピア数eをはさむ式の導出【教員採用試験 宮城県】
\( \displaystyle f(x)=x^ne^{-x} \)とする. (1) \( \displaystyle x≧0 \)での\( \displaystyle f(x) \)の最大値を求めよ. (2) \( \displaystyle n≧2 \)のとき, \( \displaystyle \left(1+\frac{1}{n}\right)^n<e< \left(1+\frac{1}{n-1}\right)^n \) を示せ. (19/3/12up) |
| 大きな数の上2桁の数【教員採用試験 栃木県】
\( \displaystyle \log_{10}2=0.3010, \log_{10}3=0.4771 \)とする. (1) \( \displaystyle \log_{10}15 \)を求めよ. (2) \( \displaystyle 12^{40} \)は何桁か (19/3/6up) |
| 妹がメネラウスの定理を証明したようです
妹シリーズ3作目です.(19/3/3up) |
| フェルマーの小定理 【教員採用試験 大阪府】
\( \displaystyle p \)は素数,\( \displaystyle a \)と\( \displaystyle p \)は違いに素な自然数とする. (1) \( \displaystyle a, 2a, 3a, \cdots , (p-1)a \)を\( \displaystyle p \)で割った余りはすべて異なることを示せ. (2) \( \displaystyle a^{p-1} \)は\( \displaystyle p \)の倍数であることを示せ. (3) \( \displaystyle 2018^{1800} \)を\( \displaystyle 181 \)で割った余りを求めよ. (19/3/3up) |
| 12分の1面積公式【教員採用試験 北海道】
点\( \displaystyle \text{P} \)から放物線\( \displaystyle y=x^2 \)へ2本の接線がひけるとき,2つの接点を\( \displaystyle \text{A}, \text{B} \)とし,線分\( \displaystyle \text{PA},\text{PB} \)及びこの放物線で囲まれる図形の面積を\( \displaystyle S \)とする.\( \displaystyle \text{PA}, \text{PB} \)が直交するときの\( \displaystyle \text{S} \)の最小値を求めよ.(19/2/28up) |
| 定積分の処理【東京大学2019年理系 第1問】
\( \displaystyle \small \int_{0}^{1}\!\!\left(x^2+\frac{x}{\sqrt{1+x^2}}\right)\!\left(1+\frac{x}{(1+x^2)\sqrt{1+x^2}}\right)dx \) そこそこ計算量があって大変です.(19/2/26up) |
| 面積 回転体の体積 【教員採用試験 東京都】
\( \displaystyle f(x)=x\sqrt{4-x^2} \) \( \displaystyle (0≦x≦2) \) (1) 関数\( \displaystyle y=f(x) \)の最大値を求めよ. (2) 関数\( \displaystyle y=f(x) \)のグラフと直線\( \displaystyle y=x \)の共有点の\( \displaystyle x \)座標を求め,それらが囲む図形の面積を求めよ. (3) (2)の図形を\( \displaystyle x \)軸周りに1回転してできる立体の体積を求めよ.(19/2/26up) |
| 今年のクリスマスは何曜日?【カレンダーを使わない計算方法】
4/4,6/6,8/8,10/10,12/12 5/9, 7/11, 9/5,11/7 は常に曜日が同じになります(2019年は木曜日).これを利用して曜日を素早く答える計算方法です.(19/2/26up) |
| 一次不定方程式、3つの解法
センター試験2019で出題された一次不定方程式 \( \displaystyle 49x-23y=1 \) を満たす整数解について, (1)数学Aの教科書風(ユークリッドの互除法) (2) まとまりをつくる方法 (3) 行列を使う方法 の3つの解き方を紹介しました.(19/2/20up ) |
| 妹が正弦定理を証明したようです
妹シリーズ2作目.(19/2/16up) |
| この机はいつのもの?【指数・対数関数の導入】
放射性炭素の性質を利用した年代測定法の話です.(19/2/16up) |
| 2次関数が3点で決まることとQRコードの話
符号理論の話です.2015年8月撮影したものの再up .(19/2/13up) |
| 級数の処理【数学検定1級 過去問】
\( \displaystyle \lim_{n\to \infty}\sum_{k=1}^{n}\frac{1}{\sqrt{2nk-k^2}}=? \) 高校範囲でOKな計算です.(19/2/13up) |
| 和算【数学検定1級 過去問】
面白い問題です.微積分の力で計算してみました.(19/2/12up) |
| 放物線ヨコ平行移動が式と逆な感じがする話題をサマータイムと絡めて話してみた
オリンピック関係でサマータイムの話題があった2018年夏に撮影したものです.(19/2/10up) |
| 分母が4次式の級数計算
\( \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}\frac{k}{k^4+4}=? \) 自作で作ってみました.(19/2/5up) |
| 妹がチェバの定理を証明したようです
妹シリーズ1作目です.(19/2/4up) |
| 1+0の無限乗の処理
\( \displaystyle \lim_{n\to\infty}\left(\frac{n+\frac{1}{2}}{n-\frac12}\right)^n=? \) ネイピア数関連の極限の処理です.(19/2/4up) |
| 三平方の定理 実験
リアル教材です.(19/2/3up) |
| 空き缶の重さを2の12乗根ずつ重くして楽器を作ってみた
モンスター(エナジードリンク)に水を入れて楽器っぽくしました.(19/2/3up) |
| 奇数・偶数n個ずつの比の極限
\( \displaystyle \lim_{n\to\infty}\frac{1\cdot 3\cdot 5\cdots(2n-1)}{2\cdot 4\cdot 6\cdots (2n)}=? \) うまく処理しましょう.(19/2/3up) |
| ペットボトルでまとめる三角関数
ペットボトルにひもを巻きつけて三角関数の公式 \( \displaystyle \sin(\theta-90^{\circ})=\cos\theta \) \( \displaystyle \cos(\theta-180^{\circ})=-\cos\theta \) などの公式を表現しました.(19/2/2up) |
| logの入った方程式の整数解
整数解を求めよ. \( \displaystyle x\log 360-y\log 48-z\log 225+\log10=0 \) 自作してみました.(19/2/2up) |
| リーマン予想と同値な不等式【数式鑑賞会】
160年ほど未解決のリーマン予想.このリーマン予想と同値な条件が高校範囲で言えるという話です.(19/2/1up) |
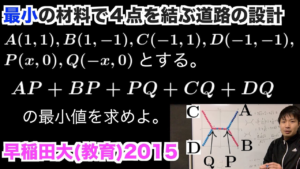
| 最小の材料で4点を結ぶ 早稲田大(教育)2015
お気に入りの問題です.直感に反する答えが出るのが面白い.(19/1/31up) |
| サンプリング定理【数式鑑賞会】
\( \displaystyle F(\xi)=\frac{R}{\sqrt{2\pi}}\sum_{n=-\infty}^{\infty}f(nR)e^{-inR\xi} \) の意義について話しました.(19/1/30up) |
| うまい棒の重さを調べてみた【標準偏差の導入】
標準偏差の導入用です.(19/1/30up) |
| 球の体積公式の微分が表面積になっている理由
微分を図形的に考えてみた話です.(19/1/29up) |
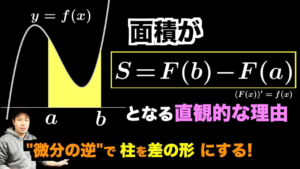
| “微分の逆”で面積がでる直観的理由
直感的な理由を説明.(19/1/28up) |
| 階乗n!を含む比の極限【数学検定1級 過去問】
\( \displaystyle \lim_{n\to\infty}\frac{n}{\sqrt[n]{n!}}=? \) 高校範囲でイケます.(19/1/27up) |
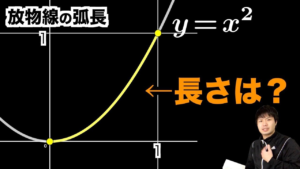
| 放物線の”長さ”を計算してみた
誘導をつければ大学入試でも出せそうです.(19/1/26up) |
| 数学検定1級 定積分【高校数学で計算できる】
\( \displaystyle \int_{-1}^{1}\frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}dx=? \) ごちゃごちゃしてますが,やることはいつも一緒です.(19/1/23up) |
| 級数クイズ【数学検定1級過去問】
\( \displaystyle \sum_{n=1}^{\infty}\frac{n^3}{n!}=? \) 宿題もつけてみました.(19/1/23up) |
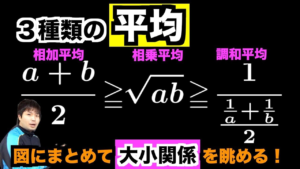
| 3種類の“平均”を紹介します(相加平均・相乗平均・調和平均)
1枚の図にまとめて大小関係を比較できるようにしました.結構好きな説明です.(19/1/22up) |
| 10033/12877は約分できるか【数学検定1級過去問】
\( \displaystyle \frac{10033}{12877} \) の約分をテーマにして,ユークリッドの互除法についての説明をしました.(19/1/17up) |
| cos42°の値 【数学検定1級過去問】
\( \displaystyle \cos 42^{\circ} \)の計算をしました.(19/1/16up) |
| ギターと12乗根のはなし
ギターと\( \displaystyle \sqrt[12]{2} \)の話です.(19/1/10up) |
| 三角関数なんか役にたたねぇぇぇ
CTスキャンの話をしました.(19/1/7up) |
| 地球の大きさ 昔の人はどう計算したか
地学基礎の教科書に乗ってる話です.(19/1/6up) |
| 「微分が正なら単調増加」を平均値の定理から導く
平均値の定理を使います.(18/12/31up) |
| 高校教科書のlogの公式を全部証明してみた
\( \displaystyle \log \)の定義からはじめ,教科書内にある公式を全部証明してみました.(18/12/28up) |
| 相関係数の値は-1以上1以下である
相関係数が\( \displaystyle -1 \)以上1以下であるというのは,数学1教科書では証明がなされていませんので今回示してみました.コーシーシュワルツの不等式から示すことができます.(18/12/28up) |
| 「1/6面積公式」をパズル的に導く
直接的な方法でなく,面積の差として計算してみました.(18/12/23up) |
| 代入前の因数分解 センター数学
多項式に数値を代入場合、くくるなどしてから計算した方が楽になることがあります.(18/12/20up) |
| 複雑な数値の大きさ比べ センター数学
\( \displaystyle \frac23 \)と\( \displaystyle \frac{3+\sqrt2}{7} \)はどちらが大きいかをシステマチックに調べる方法.実際のセンター試験で登場した数値です.(18/12/17up) |
| 放物線の接線公式 センター数学
放物線\( \displaystyle y=ax^2+bx+c(=f(x)) \)上の\( \displaystyle (m.f(m)) \)における接線の方程式は \( \displaystyle y=f'(x)x+c-am^2 \) となります.頻繁に使うので覚えておいてもいいかも,という話題です.(18/12/12up) |
| ネイピア数eの有理数乗は無理数
高校範囲で,ネイピア数\( \displaystyle e \)(とその有理数乗が)無理数であることを示します.(18/12/9up) |
| 完全順列の計算〜”よい席替え”の仕方は何通り?〜
“同じ席になる人がいないような席替え”の仕方を完全順列といいます.この計算をやってみました.(18/12/5up) |
| 円周率πが無理数であることを高校数学の範囲で証明【修正版】
高校範囲で示してみました.巧みな式変形です. (18/12/5up) |
| 自然数での値が全て素数になるような多項式は存在しない
結論としては「ない」です.その証明と,ルビー多項式という素数を多く返してくれる二次式について紹介.(18/12/3up) |
| 四元数の範囲で二次方程式を解くと無限個の解が!
高校範囲ではないですが,こんな世界もあるということで紹介.複素数より数の範囲を広げた四元数の範囲では交換法則が崩れ,また\( \displaystyle 2 \)次方程式に無数個の解がある場合があるなど通常の世界では考えられなかったような結果がでてきます.(18/12/3up) |
| ネイピア数eの登場シーンと収束性
ネイピア数\( \displaystyle e \)がどんな場面で登場するのかと,その収束性の証明です.(18/12/2up) |
| 72の法則 〜10万円が20万円に増えるのが何年後か簡単に計算する方法〜
\( \displaystyle \log \)を利用して,資産が倍になるのがなん年後か計算する公式を導きます.(18/12/1up) |
| log2の値【数値計算】東京大学2007年理系第6問
曲線で囲まれた領域を台形で近似する手法.東京大学2007年理系の問題がベースになっています.(18/11/29up) |
| 月に3万円ずつ貯めると…積立運用の計算【等比数列の和】
つみたてNISAを意識して話しました.(18/11/27up) |
| 曲率半径 〜曲線の曲がり具合を計算する〜
曲線の曲がり具合を表す曲率半径の公式を導きました.(18/11/25up) |
| sin1°の値
3次方程式の解の公式を用います.(18/11/24up) |
| sin3°の値を計算する
sin1°の計算に向けての準備.(18/11/23up) |
| 3次方程式の解の公式
3次方程式の解の公式の導出です.(18/11/22up) |
| 【四色問題】どんな地図でも4色で塗り分け可能
四色定理は難しいのでそれを妥協して”五色定理”を示しました.(18/11/17up) |
| k乗の和の公式【積分で出す】【ベルヌーイ数】
\( \displaystyle 1^k+2^k+3^k+\cdots+n^k \) について,\( \displaystyle k=1,2,3,\cdots \)の公式を積分で次々と計算する方法を紹介.(18/11/9up) |
| バーゼル問題を高校数学で解く
高校範囲で \( \displaystyle \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6} \) を導きます.(18/11/5up) |
| 分割数とオイラーの恒等式
分割数の公式です.(18/11/4up) |
| 統計学 仮説検定の考え【新数学1】
二項分布を自作し,それをもとに仮説検定を行った動画です.学習指導要領解説が元ネタです.(18/11/2up) |
| 平面グラフには次数が5以下の点が必ずある
オイラーの多面体定理から存在が保証されます.(18/11/1up) |
| 実数は有理数より”たくさんある” 【濃度の話】
高校の教科書でもちょっと意識して書かれているようです.(18/10/31) |
| 関数,写像,対応とは
用語の説明.(18/10/30up) |
| ユークリッドの互除法&1次不定方程式特殊解の手順まとめ
アルゴリズムをスライドで紹介.(18/10/29up) |
| ユークリッド互除法のアルゴリズム
ホワイトボードで説明.(18/10/26up) |
| オイラーの多面体定理の証明【数学A】
説明といった方がいいかもですが,方針はわかると思います.(18/10/25up) |
解析学(微分積分)など 54本
| 一様収束しないがlimとインテグラルが交換できる例【教員採用試験 新潟県】
関数列\( \displaystyle f_n(x)=nx(1-x)^n \) (\( \displaystyle 0≦x≦1 \))\( \displaystyle (n=1,2,3,\cdots) \)について (1) 関数列\( \displaystyle f_n \)は\( \displaystyle n\to\infty \)のとき区間\( \displaystyle I=[0,1] \)上各点収束するが一様収束しないことを示せ. (2) \( \displaystyle \lim_{n\to\infty}\int_{0}^{1}f_{n}(x)dx \)を求めよ. |
| 「曲線の長さ」=「その下の面積」となる曲線はカテナリー【数学検定1級過去問】
カテナリー(懸垂線)\( \displaystyle y=\frac{e^x+e^{-x}}{2} \)を導きます.数学3の教科書にもカテナリーの話題がちょこっとかいてあります.(19/5/18up) |
| Arctan (タンジェントの逆関数)の公式
\( \displaystyle \text{Arctan}A+\text{Arctan}B=\text{Arctan}\frac{A+B}{1-AB} \) (ただし,左辺の和の絶対値が\( \displaystyle \frac{\pi}{2} \)以下とする) 数学検定でときどき出てきたような記憶.(19/3/23up) |
| ディリクレ積分を利用した広義積分の計算【数学検定1級 過去問】
広義積分\( \displaystyle \int_{0}^{\infty}\frac{1-\cos 2x}{x^2}dx \)を計算せよ.ただし,必要ならば\( \displaystyle \int_{0}^{\infty}\frac{\sin x}{x}dx=\frac{\pi}{2} \)を使ってよい. (19/3/21up) |
| 分母が4次の級数計算【数学検定1級 過去問】
\( \displaystyle \sum_{k=1}^{\infty}\frac{k}{1+k^2+k^4}=? \) まずはあの変形です.(19/3/15up) |
| ディリクレ積分∫(sin x)/x dx【複素関数論による計算】
\( \displaystyle \int_{0}^{\infty}\frac{\sin x}{x}dx=\frac{\pi}{2} \) を複素関数論の力で計算します.(19/3/14up) |
| sin(z)=2の解【数学検定1級 過去問】
実数の範囲だと解はありませんが,複素数の範囲だと\( \displaystyle \sin z=2 \)には解があります.(19/3/6up) |
| 分母が(2のべき×n)の級数計算【数学検定1級 過去問】
\( \displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n\cdot n}=? \) 分母に\( \displaystyle n \)が来ているので,あの処理です…(19/2/26up) |
| cosx+cos2x+cos3x+…+cosnxを閉じた形で表す
オイラーの等式\( \displaystyle e^{ix}=\cos x+i\sin x \)を利用してコサインの和\( \displaystyle \cos x+\cos 2x +\cos 3x+\dots +\cos nx \)を計算する方法です.(19/2/15up) |
| フレネル積分【複素関数論による計算】
\( \displaystyle \int_{0}^{\infty}\cos (x^2)dx\) を複素関数論の力を使って計算します.(19/2/14up) |
| 連続関数にsin(∞x)を引っ掛けた積分はゼロになる【リーマン・ルベーグの定理】
どんな連続関数\( \displaystyle f(x) \)に対しても \( \displaystyle \lim_{t\to\infty}\int_{a}^{b}f(x)\sin tx dx=0 \) が成り立つ. サインの激しい揺れによって元の関数\( \displaystyle f(x) \)がなんであっても積分ゼロにさせられるという面白い結果です.コメント欄に電気信号についての関連話題があり,勉強になりました.(19/2/8up) |
| 無限に伸びる領域の面積【広義積分の計算】
広義積分の話です.(19/2/7up) |
| 誘導付きガウス積分の計算【数学検定1級 過去問】
うまく作られた問題です.積分と微分演算子の交換を保証するために一様収束であればよい、という話も少ししています.(19/2/6up) |
| フーリエ変換でわかること
フーリエ変換 \( \displaystyle \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(t)e^{-itx}dt \) が何を表しているのかを背伸びして解説.もう少し深めた解説ができるようにしたい.(19/1/29up) |
| logの和の極限【数学検定1級 過去問】
\( \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}\log\left(1+\frac{k}{n^2}\right)=? \) テイラー展開を知らないと難しいかも.(19/1/29up) |
| 垂らしたひもが作る曲線の計算【カテナリー】
微分方程式を作って関数の形を導きます.(19/1/25up) |
| この級数は収束するか?【ダランベールの判定法】
\( \displaystyle \sum_{n=1}^{\infty}\frac{1\cdot 3\cdot 4 \cdots (2n-1)}{3\cdot 6\cdot 9\cdots (3n)} \) 級数の収束判定法であるダランベールの判定法の活用です.(19/1/22up) |
| ベルヌーイ型 微分方程式の解き方
\( \displaystyle y’+P(x)y=q(x)y^n \) の形の微分方程式をベルヌーイ型といいます. |
| 1階線型微分方程式の解き方
\( \displaystyle \frac{1}{\cos x}\frac{dy}{dx}+\frac{3}{\sin x}y=1 \) 1階線型という形の微分方程式の解き方を解説.(19/1/20up) |
| 変数分離形の微分方程式の解き方
微分方程式で最初にやる型である,変数分離形の説明です.(18/11/19) |
| スターリングの公式【概要欄に訂正箇所記載】
\( \displaystyle \frac{n!}{\sqrt{2n\pi}\cdot n^n\cdot e^{-n}}\to1 (n\to \infty) \) \( \displaystyle n! \)の評価を使いやすい関数で置き換えることができる公式です.(19/1/19up) |
| 整級数の計算【数学検定1級過去問】
\( \displaystyle \small f(x)=1^2x+2^2x^2+3^2x^3+4^2x^4+\cdots \) を簡単にせよ.(19/1/18up) |
| ガンマ関数・ベータ関数の関係式
\( \displaystyle B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} \) ガンマ関数とベータ関数を結びつける公式です.(19/1/14up) |
| ガウス積分をウォリスの公式等から導く
ガウス積分 \( \displaystyle \int_{0}^{\infty}e^{-x^2}dx=\frac{\sqrt{\pi}}{2} \) をウォリスの公式などから導きます.(19/1/12up) |
| ベータ関数の定義と収束性、1/6公式
ベータ関数 \( \displaystyle \int_{0}^{1}t^{x-1}(1-t)^{y-1} \) の積分が収束することについて話をしました.(19/1/10up) |
| ガンマ関数の定義と収束性
ガンマ関数 \( \displaystyle \int_{0}^{\infty}e^{-t}t^{x-1}dt \) の収束性と,階乗の一般化になっていることについて話しました.(19/1/9up) |
| 2のベキと二項係数との壮絶な戦い
(19/1/7up) |
| ウォリスの公式 〜奇数と偶数の壮絶な戦い〜
ウォリス積分\( \displaystyle \int_{0}^{\frac{\pi}{2}}\sin^nxdx \)から導きます.(19/1/3up) |
| 交代級数の収束
\( \displaystyle a_0-a_1+a_2-a_3+\cdots \) は\( \displaystyle |a_n|\to 0 \)のとき収束するということを示しました.(19/1/1up) |
| 正項級数の収束判定法(ratioテスト)
正項級数\( \displaystyle \sum a_n \)について. \( \displaystyle \lim_{n\to \infty}\frac{a_{n+1}}{a_n} \)が1より小さいならば\( \displaystyle \sum a_n \)は収束. \( \displaystyle \lim_{n\to \infty}\frac{a_{n+1}}{a_n} \)が1より大きいならば\( \displaystyle \sum a_n \)は発散 ということを示します.(18/12/16up) |
| 重積分の極座標変換
二重積分の定義を確認し,3次の微小量の項がゼロになる説明もしてみました。(18/12/11up) |
| 解析学の基礎11 テイラーの定理 〜関数を多項式でマネする基礎理論〜
テイラーの定理を導きました.(18/12/26up) |
| 解析学の基礎10 コーシーの平均値定理をロルの定理から導く
ロルの定理の言い換え,といってもよいかもしれません.(18/12/24up) |
| 解析学の基礎09 平均値の定理をロルの定理から導く
やはり,ロルの定理が基本的ですね.(18/12/21up) |
| 解析学の基礎08 ロルの定理
連続関数は有界閉区間上で最大値をもつということを使ってロルの定理を示します.(18/12/19up) |
| 解析学の基礎07 有界閉区間上の連続関数は最大値をもつ
点列コンパクトという概念を利用して証明します.(18/12/14up) |
| 解析学の基礎06 点列コンパクトとは
点列コンパクトという概念を説明します.(18/12/13up) |
| 解析学の基礎05 コーシー列は収束する
コーシー列(基本列とも)が収束することを示します.実数の性質の1つです.(18/12/6up) |
| 解析学の基礎04 有界数列は収束部分列をもつ ボルツァーノ・ワイヤストラスの定理
これも実数の性質の1つです.(18/12/6up) |
| 解析学の基礎03 区間縮小法
実数の性質の言い換えシリーズ.(18/11/12up) |
| 解析学の基礎02 上に有界な単調増加数列は収束する
実数の性質です.上限\( \displaystyle \sup \)の存在を認めて,そこから表題の性質を導きます.(18/11/3up) |
| 解析学の基礎01 イプシロン-エヌ論法はなぜ必要か
イプシロン-エヌ論法がないと証明が困難になる状況を説明しました.(18/11/25up) |
| 【バーチャル解説】ガンマ関数とベータ関数について(後編)
VTuber流行りに乗ってみた動画.(18/11/21up) |
| 【バーチャル解説】ガンマ関数とベータ関数について(前編)VTuber流行りに乗ってみた動画.(18/11/6up) |
| カテナリー(懸垂線)の式を導く
微分方程式を立てて,ときます.(18/11/19up) |
| 留数定理を利用して実関数の積分を計算する
留数定理によって \( \displaystyle \int_{-\infty}^{\infty}\frac{dx}{x^2+1} \) を計算します.(18/11/18up) |
| ローラン展開と留数定理
ローラン展開できることをスタートにして,留数定理を導きました.(18/11/16up) |
| コーシーの積分定理
正則な範囲で閉曲線上の線積分の値が0となる,という基本的な定理を示しました.(18/11/14up) |
| 複素積分
線積分の話です.(18/11/12up) |
| 合成関数の微分【修正版】
高校教科書で曖昧に書かれているところを説明.(18/11/10up) |
| リーマンゼータ関数を解析接続する手順
解析接続するまでの道筋を示したものですが,未だ(2019年8月時点)解説動画ができていません.(18/11/4up) |
| 対数関数のテイラー展開 log(1+x)
\( \displaystyle \log (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots \) を導きます.(18/10/27up) |
| 一様収束するなら連続性は保たれる【解析学】
連続関数列\( \displaystyle \{ f_n\} \)が\( \displaystyle f \)に一様収束するとき,\( \displaystyle f \)は連続であることを示しました.(18/10/26up) |
| 一様収束でうれしいこと【解析学】
一様収束なら連続性が保たれること(次の動画で紹介),インテグラルとlimの交換ができることを示しました.(18/10/24up) |
代数学など 20本
| 群になれなかった集合たちへ名前をつける【マグマ・半群・モノイド】群から条件を緩めていったクラスにも名前がある.(19/6/4up) |
| (-2)×(-3)=6を環の定義から導く
そもそも\( \displaystyle -2 \)とは何か?など数の定義を把握することの重要せいを思い知らされます.(19/5/19up) |
| 群の定義をそぎ落とす!【群論基礎演習】
群の定義の単位元の存在および各元に対する逆元の存在条件を若干ゆるくしても同値であるという話題です.抽象的なことしか仮定していないのに豊富な結果が得られるのは不思議です.(19/5/17up) |
| 一次関数の集合は合成に関して群になる【群論基礎演習】
1次関数の集合 \( \displaystyle G=\{\phi :R\to R|\exists a(\not= 0)\in R, b\in R, \) \( \displaystyle \hspace{7em} \forall x\in R,\phi(x)=ax+b \} \) は合成に関して群になることを示せ.(19/5/13up) |
| 有理数の構成【教員採用試験 香川県】
代数の議論に慣れていると難しくないです.(19/3/17up) |
| 群論15 7の2019乗の下3桁の計算
\( \displaystyle 7^{2019} \)の下3桁を群論の力を利用して計算しました.(19/2/10/up) |
| 群論14 有限集合に対する部分群判定条件
\( \displaystyle a,b\in H\Rightarrow ab\in H\) 有限の場合、群であるための条件は上の形にゆるめられるということを示しました.(19/1/21up) |
| 群論13 準同型定理
\( \displaystyle G/\ker f \cong G’\) 準同型定理の証明です.もとの群\( \displaystyle G \)をカーネル\( \displaystyle \ker G \)で割った剰余群と準同型像\( \displaystyle f(G)=G’ \)が同型という定理です.(19/1/14) |
| 群論12 カーネル(核)の定義と性質 群論
準同型写像で単位元にとぶような元の集合をカーネルといいます.このカーネルが正規部分群であることを示しました. |
| 群論11 準同型写像の定義と性質
演算を保存する写像 \( \displaystyle f(ab)=f(a)f(b) \) を準同型写像といいます.この定義と性質を紹介しました.(19/1/11up) |
| 群論10 剰余群
加法群Z/nZが群Zを正規部分nZで考えたときの剰余群となっているという点を例示しました。(19/1/7up) |
| 群論09 正規部分群 〜安心して剰余類の演算定義を〜
\( \displaystyle aH=Ha \) 剰余類を元と考え演算を定義できるための条件を考えます.(19/1/5up) |
| 群論08 剰余類の演算定義の問題点 〜正規部分群の導入〜
剰余類に対して演算を定義するとはどういうことか?を考えました.(19/1/2up) |
| 群論07 対称群S3を具体的に分解(班分け)してみよう
剰余類の代表元はその類に属する元であればどれをとってもよいという話をしました.(18/12/30up) |
| 群論06 剰余類 〜群の班分け〜
剰余類をつくるとどれも元の個数(濃度)が同じであることが示せます.群は抽象的に定義されたものですが,ここまで豊富な結果が得られるのが不思議です.(18/12/26up) |
| 群論05 群の例 〜対称群〜
具体的な群の例として対称群\( \displaystyle S_3 \)を扱います.(18/12/23up) |
| 群論04 合成写像の性質(全単射や結合法則など)
・2つの単射写像の合成は単射 ・2つの全射写像の合成は全射 ・合成という演算は結合法則を満たす ことを示しました.(18/12/21up) |
| 群論03 部分群の判定に便利な条件
\( \displaystyle G \)の部分集合\( \displaystyle H \)が\( \displaystyle G \)の部分群であるためには, 「\( \displaystyle \forall a, b \in H \Rightarrow a^{-1}b\in H \)」 が必要十分であることを示しました. |
| 群論02 部分群の単位元・逆元はもとの群のものと一致する
群\( \displaystyle G \)の単位元\( \displaystyle e \)と\( \displaystyle G \)の部分群\( \displaystyle H \)の単位元\( \displaystyle e’ \)は同じである. 群\( \displaystyle H \)の元\( \displaystyle a \)の,\( \displaystyle G \)における逆元と\( \displaystyle H \)における逆元は同じである. ことを示します.(18/12/15up) |
| 群論01 群の定義と性質
群の定義です.(18/12/9up) |
確率・統計など 9本
| 確率8 初成功までの失敗回数の分布 幾何分布
幾何分布 \( \displaystyle P(X=k)=pq^k \) の平均・分散の計算です. 初成功までの試行回数を幾何分布とする流儀もあります。この流儀の方を、日本アクチュアリー会では「ファーストサクセス分布」と呼んでいるようです(かっこいい) (19/5/12up) |
| 確率7 たまに発生する事象の確率分布 ポアソン分布
ポアソン分布 \( \displaystyle P(X=k)=\frac{{\lambda}^k}{k!}e^{-\lambda} \) を二項分布から導きます.(19/4/11up) |
| 確率6 積率母関数の利用
\( \displaystyle M_{X}(t)=E(e^{tX}) \) 平均や分散を求める際に使える道具です.(19/3/23up) |
| 確率5 二項分布の期待値,分散を定義から求める
\( \displaystyle P(X=k)=_{n}C_{k}p^{k}q^{n-k} \) 二項分布の平均・分散を定義から計算します.二項係数の処理がちょっとごちゃっとします.(19/3/19up) |
| 確率4 分散と標準偏差
分散\( \displaystyle V(X)=E((X-E(X))^2) \)と標準偏差\( \displaystyle \sigma(X)=\sqrt{V(X)}\)について (19/3/9up) |
| 確率3 期待値の線型性
\( \displaystyle E(aX+b)=aE(X)+b \) を示します.(19/2/26) |
| 確率2 確率変数の期待値
離散変数,連続変数の期待値(平均)の計算です.(19/2/23up) |
| 確率1 確率密度関数
連続的な確率変数についての話です.(19/2/18up) |
| 区間 [0,1]から任意に選んだ2数の差が0.3以上になる確率【数学検定1級 過去問】
数直線上の0と1の間で任意に2つの値\( \displaystyle x,y \)を選ぶとき,それらが \( \displaystyle |x-y|≧0.3 \) を満たす確率を求めよ. (19/2/9up ) |
線型代数など 9本
| 線型代数8 行列の正則性と行列式の関係〜余因子行列を用いて〜
\( \displaystyle A \)が正則\( \displaystyle \Leftrightarrow \) \( \displaystyle |A|\not= 0 \) を余因子行列を用いて示します.説明が難しいです.(19/3/15up) |
| 線型代数7 積の行列式
\( \displaystyle |AB|=|A||B| \) の証明です.説明が難しいです.(19/3/10up) |
| 行列式の計算問題【数学検定1級 過去問】
対称的な形ですね.(19/3/7up) |
| 線型代数6 行列式の性質
行列式の基本性質 ・2つの行を入れ替えると\( \displaystyle -1 \)倍 ・同じ行があると0 ・行のc倍は全体のc倍 ・行の和は分けて良い ことを示します.(19/3/3) |
| 線型代数5 行列式の余因子展開
4次の行列式を3次に表す場合で示しました.線型代数は説明が難しいです.(19/2/28) |
| 線型代数4 行列式の定義
置換を用いた行列式の定義です.行から1個ずつ選ぶという感じを掴みましょう.(19/2/24up) |
| 線型代数3 置換の符号(sgn)
置換の意味とその計算方法です.(19/2/22up) |
| 線型代数2 二次の行列
\( \displaystyle \left( \begin{array}{cc}a & b \\ c & d \\ \end{array} \right)^{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc}d & -b \\ -c & a \\ \end{array} \right) \) を示します.一昔前の数学Cで扱っていた内容です.(19/2/20up) |
| 線型代数1 行列の積
行列の積について.なぜそんな計算を考えるんだ?という疑問を持ちやすいので,行列の積が登場するシーンを紹介.(19/2/19up) |
| グラム・シュミットの直交化法
ベクトルたちを「どの2つのベクトルも直交」していて「大きさが1」にする計算方法です.(19/1/3up) |
撮影環境・グッズ・その他 19本
| 実験 白いマーカーはチョークの代わりにできそう
黒板シートに対して白マーカーが有効か試してみた.(19/6/2up) |
| “黒板”を新しくしました【3500円・40分】
古くなった黒板シートの張り替え作業.(19/6/1up) |
| 文字でまとめるモードに入るので更新頻度が下がります
更新を不定期に行う宣言をした.(19/4/14up) |
| 入学シーズンなのでアニソン歌います
登録者が1万人超えた日にアップした動画です.(19/4/5up) |
| 数学アプリGeoGebra スライダーの使い方と教材共有方法
数学アプリジオジェブラでのスライダーの使い方と,作った教材に簡単にアクセスさせるための手順紹介です.(19/2/25up) |
| 正規分布のおもちゃ【GALTON BOARD】
無数の細かい球を転がすことで正規分布(正確には二項分布)のできる様子を見ることができるおもちゃ紹介です.(19/2/20up) |
| 【ちびっこ向けクイズ】不等式の名前を当ててみよう!全部答えられるかな?
瀬戸弘司さんの動画パロディです.(19/2/11up) |
| 数学アプリGeoGebraで領域の図を作成する
数学アプリジオジェブラの使い方です.(19/2/9up) |
| センター試験を救いたい
センター試験を救いたくなった動画です.(19/2/5) |
| コメントありがとうございます
コメントが多くなってきたので出した動画です.(19/1/31up) |
| 俺はセンター試験に怒っているぞ!
センター試験に怒った風動画です.(19/1/21up) |
| クラッピング・カルテット
文化祭などのネタにどうぞ.(19/1/11up) |
| もしも、コサインが禁止になったら 〜余弦定理が使えなくなった世界
(19/1/9up) |
| ただの壁を黒板化する
撮影時に使っている自宅の壁の紹介.(19/1/8up) |
| 三角関数を教えるときに役立つ小道具2つ
角度・長さを表現できる教材「くるくる君」と,正確な角度を黒板上で表現するフィルムの紹介です.(19/1/6up) |
| おさそい
ユーチューブへのお誘いです.登録者120人ほどのときの動画です.(19/1/4up) |
| 【ちびっこ向けクイズ】曲線の名前を当ててみよう!全部答えられるかな?
いろいろな曲線に関するクイズです.(19/1/3up) |
| 沖縄 波の上ビーチの様子です
2018年12月撮影.(18/12/9up) |
| 式変形チャンネル方針
当チャンネル1本目の動画です.(18/10/24w ) |
英語練習 4本
| quartic equation
4次方程式\( \displaystyle (x+1)(x+4)(x+7)(x+10)+9^2=0 \)を解く.(19/6/9up) |
| Multiplying fractions
\( \displaystyle \frac45\times\frac23=\frac{8}{15} \)を説明.(19/1/5up) |
| The four arithmetic operations
四則演算について.(18/12/24up) |
| Brief introduction
はじめてみた.(18/11/19up) |
| ときどき英語で喋る動画出すかもしれません
予告.(18/11/17up) |